放在开头的话
1.本人1月13日才刚刚接触了淀粉汁,所以可能很多东西没有理解完全甚至出错,如果您有什么疑问的话,请发在下面的评论区。
2.淀粉汁是跟着一篇题解学的,因此可以有些代码很像,但是原来题解的部分没讲到的地方我可能会提出来
3.这东西目前可能会更的很慢
初级
什么是点分治?
点分治是处理树上问题的一种高效的办法,时间复杂度很优秀,而且思想比较巧妙。
怎么来做呢?
首先我们引入树的重心
树的重心
树的重心也叫树的质心。找到一个点,其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心,删去重心后,生成的多棵树尽可能平衡。
什么意思呢?
我们可以从这里推得以树的重心为根的任意一颗子树大小不超过n/2
证明就不用了吧
于是我们求log2N次重心,那么每个点就能被确定了。
于是时间复杂度就变成了O(NlogN)
怎么求呢?
根据它的定义,树的重心一定是最大子树最小的点。
感性理解即可
于是照着求就可以了啊。
但是我们要多次求,因此我们得加一个条件,判断是否可以访问
vis[]或者fw[]就可以了
于是整个代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
inline void getzx(int t,int fat)
{
int i,j;
sz[t]=1;
maxp[t]=0;
for(i=head[t];i;i=e[i].next)
{
j=e[i].to;
if(j==fat||vis[j]) continue;
getzx(j,t);
sz[t]+=sz[j];
maxp[t]=max(sz[j],maxp[t]);
}
maxp[t]=max(maxp[t],tot-sz[t]);
if(maxp[t]<maxp[rt]) rt=t;
}
|
点分治怎么做
我们只需要不断寻找重心,用这些重心来计算我们要的答案
我们举个例子:
现在这里有一棵树
(假定蓝色是未被处理的点,红色是当前子树的重心,绿色是处理完的点)

先找到全局重心
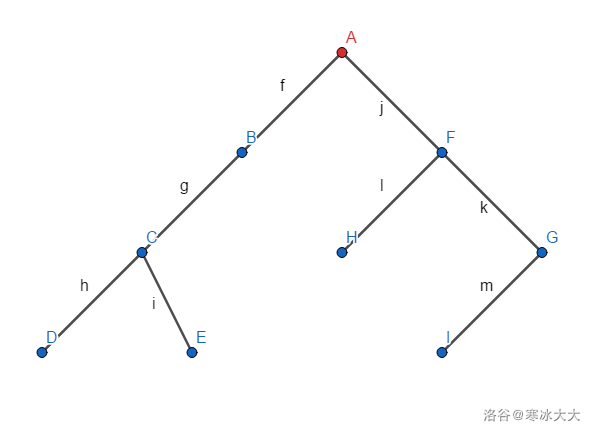
然后对他的子树,也这样找
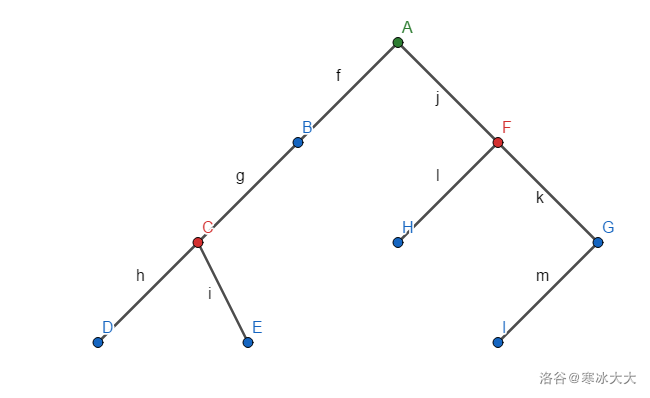
一直接下去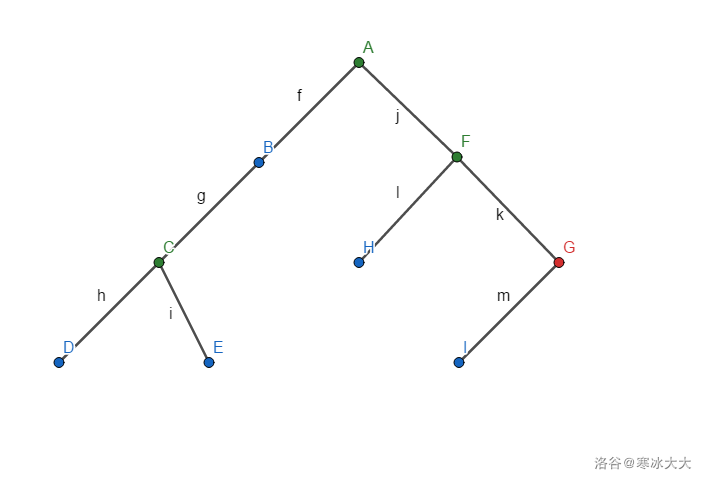
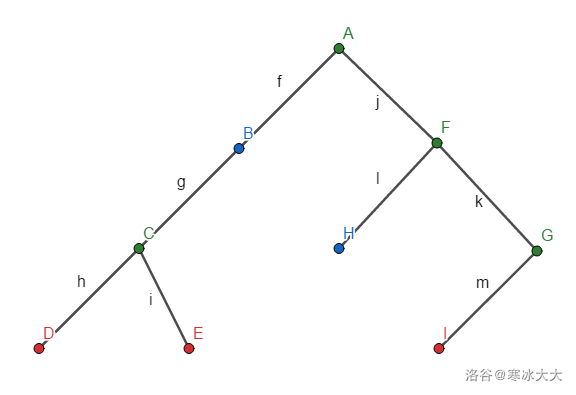
然后做完了。
等一下,这不是大部分点都被扫过了吗,时间复杂度怎么还会是O(NlogN)?
的确,这张图中大部分店都被扫到了,而且都求了重心,但是如果每条边中间连接1000个点,只有m,i,h三条边被处理的重心增多了。
增多了多少呢?
每条边在10左右。
现在你感性理解到了复杂度了吧
由于之前有一个推论
我们可以从这里推得以树的重心为根的任意一颗子树大小不超过n/2
每次树的大小会变得不超过原来的一般,log2N次后树的大小就会变成1,每一次最多遍历整棵树O(N),复杂度就得到O(NlogN)?了
不信?我们用随机几十组数据看看
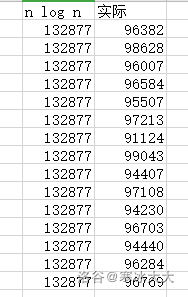
数据生成器放在这里
测试用的代码放在这里 改自P2634 [国家集训队]聪聪可可
下面是一个模板代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| inline void solve(int t)
{
int i,j;
vis[t]=judge[0]=1; calc(t);
for(i=head[t];i;i=e[i].next)
{
j=e[i].to;
if(vis[j]) continue;
tot=sz[j];
maxp[rt=0]=bign;
getzx(j,0);
solve(rt);
}
}
|
例题
P3806 【模板】点分治1
大意
给定一棵有n个点的树
询问树上距离为k的点对是否存在。
其实是很无脑的两个桶,一个judge[]和一个tmp[],judge存非本路径上长度能达到的数字,tmp[]存本路径上能达到的数字,把此时重心看做LCA,于是若tmp[]中一个数+judge[]一个数=k,就说明路径存在。
接着,这条路径遍历完后,把tmp的数字转移到judge里面
这个地方我们找完了,只需要把judge里面的数字清空即可。
于是我们就有代码了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
| #include<iostream>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<queue>
#include<stack>
#include<vector>
#include<set>
#include<map>
#include<algorithm>
using namespace std;
const int maxn=10010,bign=10001000;
int n,m,tmp[bign],judge[bign];
int sz[maxn],vis[maxn];
int head[maxn],que[maxn];
int size,maxp[maxn];
int tot,rt,dis[maxn];
int q[bign],ynn[maxn];
struct edge{
int next,to,dis;
}e[maxn*2];
inline void addedge(int next,int to,int dis)
{
e[++size].to=to;
e[size].dis=dis;
e[size].next=head[next];
head[next]=size;
}
inline void getzx(int t,int fat)
{
int i,j;
sz[t]=1;
maxp[t]=0;
for(i=head[t];i;i=e[i].next)
{
j=e[i].to;
if(j==fat||vis[j]) continue;
getzx(j,t);
sz[t]+=sz[j];
maxp[t]=max(sz[j],maxp[t]);
}
maxp[t]=max(maxp[t],tot-sz[t]);
if(maxp[t]<maxp[rt]) rt=t;
}
inline void getdis(int t,int fat)
{
tmp[++tmp[0]]=dis[t];
int i,j,k;
for(i=head[t];i;i=e[i].next)
{
j=e[i].to;
k=e[i].dis;
if(vis[j]||j==fat) continue;
dis[j]=dis[t]+k;
getdis(j,t);
}
}
inline void calc(int t)
{
int p=0,i,j,k,l;
for(i=head[t];i;i=e[i].next)
{
j=e[i].to;
k=e[i].dis;
if(vis[j]) continue;
tmp[0]=0;
dis[j]=k;
getdis(j,t);
for(k=tmp[0];k;k--)
for(l=1;l<=m;l++) if(que[l]>=tmp[k]) ynn[l]|=judge[que[l]-tmp[k]];
for(k=tmp[0];k;k--) q[++p]=tmp[k],judge[tmp[k]]=1;
}
for(i=p;i;i--) judge[q[i]]=0;
}
inline void solve(int t)
{
int i,j;
vis[t]=judge[0]=1; calc(t);
for(i=head[t];i;i=e[i].next)
{
j=e[i].to;
if(vis[j]) continue;
tot=sz[j];
maxp[rt=0]=bign;
getzx(j,0);
solve(rt);
}
}
int main()
{
ios::sync_with_stdio(false);
register int i,h;
int t1,t2,t3;
cin>>n>>m;
for(i=1;i<n;i++)
{
cin>>t1>>t2>>t3;
addedge(t1,t2,t3);
addedge(t2,t1,t3);
}
for(i=1;i<=m;i++) cin>>que[i];
maxp[rt=0]=n;
tot=n;
getzx(1,0);
solve(rt);
for(i=1;i<=m;i++)
{
if(ynn[i]) cout<<"AYE"<<endl;
else cout<<"NAY"<<endl;
}
return 0;
}
|










