Splay

呜呼今天终于搞懂splay了

学习之前你需要知道的

这东西深度并不是 log⁡n\log n 的，但是复杂度是均摊 O(nlog⁡n+mlog⁡n)O(n\log n+m\log n) 的 初学者可能会把它当做一个平衡树

基础的函数

1
2
3
4
5
6
7

	inline void pushup(int x){sz[x]=sz[ls]+sz[rs]+cnt[x];}
//字面意思
	inline int pd(int x){return c[f[x]][1]==x;}
//判断是左子树还是右子树
	inline void clear(int x){ls=rs=sz[x]=f[x]=val[x]=cnt[x]=0;}
//清空这个节点

splay的函数

rotate

1
2
3
4
5
6
7
8
9
10
11
12
void rotate(int x)
{
	int y=f[x],z=f[y],k=pd(x),m=c[x][!k];
	//其实rotate的本质就是x与子节点改变方向（因为原本在y下方的x到了y上方）
	//另外这个时候还要发现x到!k方向上的连边已经被占用了，所以我们得把这个点移到y上
	c[y][k]=m; c[x][!k]=y; f[m]=y; f[y]=x; f[x]=z;
	if(z) c[z][c[z][1]==y]=x;
    //如果z还在的话，那么肯定要连这个边啊
	pushup(x);
	pushup(y);
    //常规pushup
}

splay

1
2
3
4
5
6
7
8
9
10
11
void splay(int x)
{
	for(int y=f[x];y=f[x],y;rotate(x))
	{
		if(f[y]) rotate(pd(x)^pd(y)?x:y); 
		//如果三个节点在一个方向的话，单纯的旋转并不会改变树的高度，所以我们得用奇技淫巧来优化一下
        //这里有点不对，splay并不需要太注意树的高度，但是不这样操作的话y的父亲变成z
		rt=x;	
        //我们只需要最后一次的x为根，把这个东西卸载循环外面貌似也可以？
	}
}

BST函数

insert

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
void insert_tree(int target) 
//分三种情况讨论，一是没有根节点，二是这个数字已经在splay中，三是这个东西还没在splay中
{
	int x=rt,fat=0;
	if(!rt)
	{
		val[++tot]=target;
		cnt[tot]++;
		rt=tot;
		pushup(rt);
		return ;
	}
	while(1)
	{
		if(val[x]==target)
		{
			cnt[x]++;
			pushup(x);
			pushup(fat);
			splay(x); //记得splay
			return ;
		}
		fat=x;
		x=c[x][val[x]<target];
		if(!x)
		{
			c[fat][val[fat]<target]=++tot;
			f[tot]=fat;
			val[tot]=target;
			cnt[tot]++;
			pushup(tot);
			pushup(fat);
			splay(tot);//记得splay
			return ;
		}
	}
}

delete

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
void delete_tree(int target)
{//分五种情况，一是这个被删除的数在现在的splay中不止一个，这个时候直接--。
    //下面这些情况默认splay中只有一个
    //这个节点没有左子树，那么直接设右子树为根并且清除当前子树
    //没有右子树也同理
    //左子树右子树都没有的话，这时候只要清除并且把根设为0就行了
    //对于剩下那种情况，我们用前驱来顶替这个节点
	int looker;
	rk(target);
	int x=rt;
	if(cnt[rt]>1)  
	{
		cnt[rt]--;
		pushup(rt);
		return ;
	}
	if(!ls&&!rs)
	{
		clear(rt);
		rt=0;
		return ;
	}
	if(!ls)
	{
		looker=rt;
		rt=c[looker][1];
		f[rt]=0;
		clear(looker);
		return ;
	}
	if(!rs)
	{
		looker=rt;
		rt=c[looker][0];
		f[rt]=0;
		clear(looker);
		return ;
	}
	looker=rt;
	x=pre();
	splay(x); 
	f[c[looker][1]]=x;
	c[x][1]=c[looker][1];
	clear(looker);
	pushup(rt);
}

kth

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int kth(int k)
{
	int x=rt;
	while(1)
	{
		if(ls&&k<=sz[ls]) x=ls;
		else 
        {
			k-=sz[ls]+cnt[x];
			if(k<=0) {splay(x);return val[x];}
			x=rs;
		}
	}
}

前驱/后驱

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//根据定义，只需要找到左子树中最右边的节点就行了

int nxt()
{
	int x=c[rt][1];
	while(ls)
	{
		x=ls;
	}
	splay(x);
	return x;
}

//根据定义，只需要找到左子树中最左边的节点就行了

int pre()
{
	int x=c[rt][0];
	while(rs)
	{
		x=rs;
	}
	splay(x);
	return x;
}

rk

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int rk(int target)
{
	int x=rt,ans=0;
	while(1)
	{
		if(target<val[x]) x=ls; 
		else 
		{
			ans+=sz[ls];
			if(target==val[x]) 
			{
				splay(x);
				return ans+1;	
			}
            //这个是模板题给的rk的定义
			if(target>val[x]) ans+=cnt[x],x=rs;
		}
	}
}

整个代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<queue>
#include<stack>
#include<vector>
#include<set>
#include<map>
#include<algorithm>

#define ls c[x][0]
#define rs c[x][1]

using namespace std;

const int maxn=100100;

int sz[maxn],c[maxn][2];
int val[maxn],cnt[maxn],tot,rt;
int f[maxn];

struct ssplay{
	
	inline void pushup(int x){sz[x]=sz[ls]+sz[rs]+cnt[x];}
	inline int pd(int x){return c[f[x]][1]==x;}
	inline void clear(int x){ls=rs=sz[x]=f[x]=val[x]=cnt[x]=0;}
	
	void rotate(int x)
	{
		int y=f[x],z=f[y],k=pd(x),m=c[x][!k];
		c[y][k]=m; c[x][!k]=y; f[m]=y; f[y]=x; f[x]=z;
		if(z) c[z][c[z][1]==y]=x;
		pushup(x);
		pushup(y);
	}
	
	void splay(int x)
	{
		for(int y=f[x];y=f[x],y;rotate(x))
		{
			if(f[y]) rotate(pd(x)^pd(y)?x:y);
			rt=x;	
		}
	}
	
	void insert_tree(int target)
	{
		int x=rt,fat=0;
		if(!rt)
		{
			val[++tot]=target;
			cnt[tot]++;
			rt=tot;
			pushup(rt);
			return ;
		}
		while(1)
		{
			if(val[x]==target)
			{
				cnt[x]++;
				pushup(x);
				pushup(fat);
				splay(x);
				return ;
			}
			fat=x;
			x=c[x][val[x]<target];
			if(!x)
			{
				c[fat][val[fat]<target]=++tot;
				f[tot]=fat;
				val[tot]=target;
				cnt[tot]++;
				pushup(tot);
				pushup(fat);
				splay(tot);
				return ;
			}
		}
	}
	
	int rk(int target)
	{
		int x=rt,ans=0;
		while(1)
		{
			if(target<val[x]) x=ls;
			else 
			{
				ans+=sz[ls];
				if(target==val[x]) 
				{
					splay(x);
					return ans+1;	
				}
				if(target>val[x]) ans+=cnt[x],x=rs;
			}
		}
	}
	
	int kth(int k)
	{
		int x=rt;
		while(1)
		{
			if(ls&&k<=sz[ls])
			{
				x=ls;
			}
			else 
			{
				k-=sz[ls]+cnt[x];
				if(k<=0) {splay(x);return val[x];}
				x=rs;
			}
		}
	}
	
	int nxt()
	{
		int x=c[rt][1];
		while(ls)
		{
			x=ls;
		}
		splay(x);
		return x;
	}
	
	int pre()
	{
		int x=c[rt][0];
		while(rs)
		{
			x=rs;
		}
		splay(x);
		return x;
	}
	
	void delete_tree(int target)
	{
		int looker;
		rk(target);
		int x=rt;
		if(cnt[rt]>1)
		{
			cnt[rt]--;
			pushup(rt);
			return ;
		}
		if(!ls&&!rs)
		{
			clear(rt);
			rt=0;
			return ;
		}
		if(!ls)
		{
			looker=rt;
			rt=c[looker][1];
			f[rt]=0;
			clear(looker);
			return ;
		}
		if(!rs)
		{
			looker=rt;
			rt=c[looker][0];
			f[rt]=0;
			clear(looker);
			return ;
		}
		looker=rt;
		x=pre();
		splay(x); 
		f[c[looker][1]]=x;
		c[x][1]=c[looker][1];
		clear(looker);
		pushup(rt);
	}
		
}spl;

int n,m;

int main()
{
	ios::sync_with_stdio(false);
	register int i,j;
	cin>>n;
	int opt,x;
	for(i=1;i<=n;i++)
	{
		cin>>opt>>x;
		if(opt==1)
		{
			spl.insert_tree(x);
		}
		if(opt==2)
		{
			spl.delete_tree(x);
		}
		if(opt==3)
		{
			cout<<spl.rk(x)<<endl;
		}
		if(opt==4)
		{
			cout<<spl.kth(x)<<endl;	
		}
		if(opt==5)
		{
			spl.insert_tree(x);
			cout<<val[spl.pre()]<<endl;
			spl.delete_tree(x);
		}
		if(opt==6)
		{
			spl.insert_tree(x);
			cout<<val[spl.nxt()]<<endl;
			spl.delete_tree(x);
		}
	}
}

复杂度证明

以下的都忽略 O(1)O(1) 常数

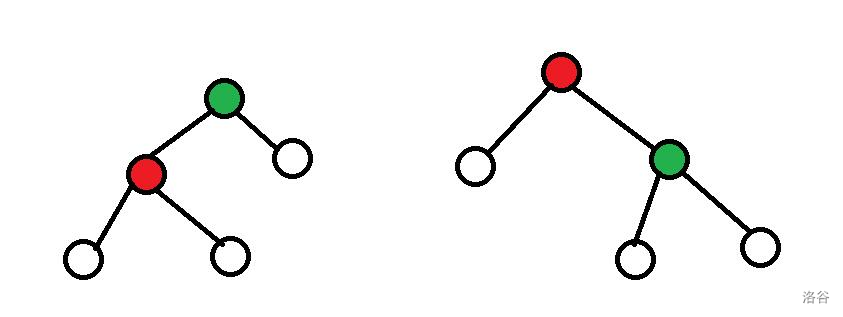
对于一次 zig\text{zig} 操作 ： 定义$ \Delta\phi(T)=\phi(x’)+\phi(y’)-\phi(x)-\phi(y)=\phi(y’)-\phi(x)\leq\phi(x’)-\phi(x)$

对于 $\text{zig zag} $ 操作

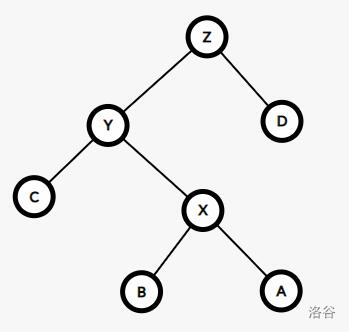
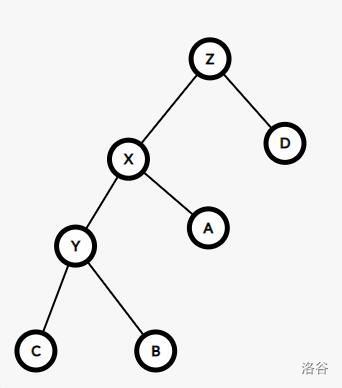
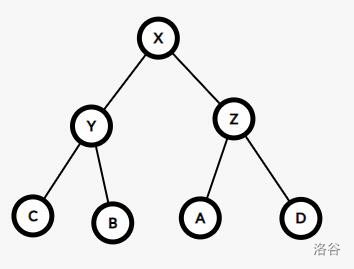
肉眼可见树的深度变小了，但是这不是平衡树

Δϕ(T)=ϕ(x′)+ϕ(y′)+ϕ(z′)−ϕ(x)−ϕ(y)−ϕ(z)=ϕ(y′)+ϕ(z′)−ϕ(x)−ϕ(y)≤ϕ(y′)−ϕ(z′)−2ϕ(x)=2(ϕ(x′)−ϕ(x))+(ϕ(y′)+ϕ(z′)−2ϕ(x′))≤2(ϕ(x′)−ϕ(x))\begin{aligned} \Delta\phi(T)&=\phi(x')+\phi(y')+\phi(z')-\phi(x)-\phi(y)-\phi(z) \\&=\phi(y')+\phi(z')-\phi(x)-\phi(y) \\&\leq\phi(y')-\phi(z')-2\phi(x) \\&=2(\phi(x')-\phi(x))+(\phi(y')+\phi(z')-2\phi(x')) \\&\leq2(\phi(x')-\phi(x)) \end{aligned}

同理，我们看看 zig zig\text{zig zig}

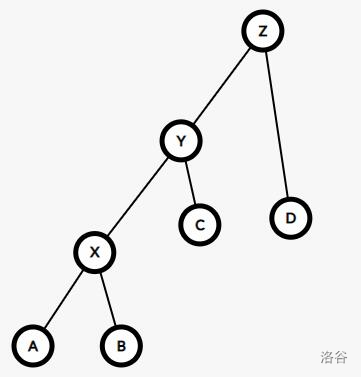
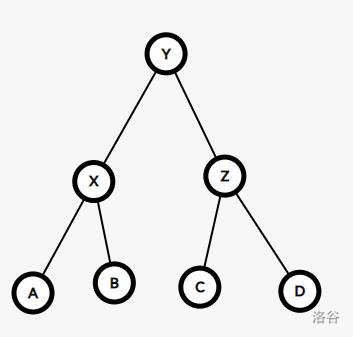
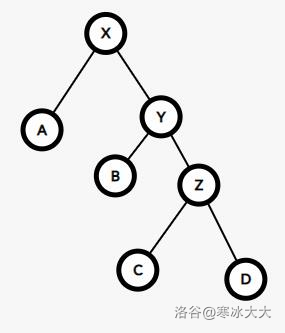
这时候的情况就稍微有一点不同了

Δϕ(T)=ϕ(x′)+ϕ(y′)+ϕ(z′)−ϕ(x)−ϕ(y)−ϕ(z)=ϕ(y′)+ϕ(z′)−ϕ(x)−ϕ(y)≤ϕ(x′)+ϕ(y′)−2ϕ(x)=3(ϕ(x′)−ϕ(x))+(ϕ(y′)+ϕ(x)−2ϕ(x′))≤3(ϕ(x′)−ϕ(x))\begin{aligned} \Delta\phi(T)&=\phi(x')+\phi(y')+\phi(z')-\phi(x)-\phi(y)-\phi(z) \\ &=\phi(y')+\phi(z')-\phi(x)-\phi(y) \\&\leq\phi(x')+\phi(y')-2\phi(x) \\&=3(\phi(x')-\phi(x))+(\phi(y')+\phi(x)-2\phi(x')) \\&\leq3(\phi(x')-\phi(x)) \end{aligned}

由于 zig\text{zig} 操作 不超过一次，因此复杂度显然是均摊 O(nlog⁡n)O(n\log n)