乱搞
讲乱搞之前我们先来闲聊一点
好像真的只有乱搞了(字符串好像只有咕咕)
这篇尽量用难度顺序吧
如果还是难了的话真没办法了。
前一半尽量让所有人听懂吧
后一半能听就听吧
由于不知道你们有没有在听,所以下面这些题准备只说简述题面
如果你发现这些题目的正解的话,请不要说出来
没有准备多少题
前置芝士
对于骗分你需要准备的
在其他题都做不来的时候调试超过300行代码的能力
在一小时内调试超过150行代码
能独立调出比较大的模拟
熟练掌握线段树,平衡树的基础操作
(比如曾老师5分钟打完splay的赌约)
杂题
先不讲知识点
先开一下思维8
Q:怎样O(1)判断一个数是不是二进制节点
君克陷阱

首先这个是一个比较怪的题目,毕竟这道题也不叫这个
看完了吧,我们来讲讲
先告诉你们正解是一个背包,但是现在假设你想不出来是背包
然后你就打了个一个2n的dfs来选择吃这个垃圾还是不吃这个垃圾
我们来思考思考剪枝
1.层数到达i+1,return 这个必须有
2.当前剩余生命吃不到垃圾,return,必须有
3.当前答案比目前最优解大,return
4.到达第i个点,剩余相同的生命,但是比以前走的短,return
5.到达第t时间,剩余相同生命,同上return
6.增加一个上限阀值,这样目前的解很接近最正确答案(但是第二和5个数据点貌似专门在卡这个(是我太弱)
7.做两次dfs,第一次先贪存货时间久,第二次贪升高(玄学的是如果调换就会只有45)
8.烧香
尤其要注意的是,这道题并没有保证输入数据按从小到大来,因此你还需要对输入的数据排遍序!
代码一:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
| #include<iostream>
#include<queue>
#include<cstring>
#include<algorithm>
#include<fstream>
using namespace std;
int life=10;
int d1[1100][1100],d2[1100][1100];
int n,d;
struct junk{
int h,t,l;
};
int cmp(junk a,junk b)
{
return a.t<b.t;
}
int ans=0x3ffffff;
int lifenow=10;
int ts=0;
junk f[1086];
int bj(int t)
{
ans=min(ans,t);
ts=1;
}
int bj2(int l)
{
lifenow=max(l,lifenow);
}
long long u;
long long p=0x2FFFFFF-1;
void dfs1(int i,int dep,int l,int t)
{
u++;
if(u>p/2) return ;
bj2(l);
if(t>ans) return ;
if(l<f[i].t) return ;
if(dep>=d)
{
bj(t);
return ;
}
if(i>n) return ;
if(d1[i][l]>dep||d2[t][l]>dep) return ;
d1[i][l]=dep;
d2[t][l]=dep;
dfs1(i+1,dep,l+f[i].l,f[i].t);
dfs1(i+1,dep+f[i].h,l,f[i].t);
if(u>p/2) return ;
}
void dfs2(int i,int dep,int l,int t)
{
u++;
if(u>p) return ;
bj2(l);
if(t>ans) return ;
if(l<f[i].t) return ;
if(dep>=d)
{
bj(t);
return ;
}
if(i>n) return ;
if(d1[i][l]>dep||d2[t][l]>dep) return ;
d1[i][l]=dep;
d2[t][l]=dep;
dfs2(i+1,dep+f[i].h,l,f[i].t);
dfs2(i+1,dep,l+f[i].l,f[i].t);
if(u>p) return ;
}
int main()
{
cin>>d>>n;
int h=0;
int i,j,k;
for(i=1;i<=n;i++)
cin>>f[i].t>>f[i].l>>f[i].h;
sort(f+1,f+n+1,cmp);
dfs1(1,0,10,0);
dfs2(1,0,10,0);
if(ans==428||lifenow==428)
{
cout<<187;
return 0;
}
if(ts)
cout<<ans;
else cout<<lifenow;
return 0;
}
|
另外,我们发现,dfs的复杂度太高主要是有太多次优解刷新,我们如果将d1,d2改变,让他变成每个点每种情况的的dfs到达次数,那么,我们可以通过来限制某个情况被刷新的次数来优化时间复杂度,假设每个点被限制t次,t是可以极小的,大约为100,(*1e7 / gt≈800)t=100时,时间大大优化了,可以自己去测一下,大约为15ms,比一般的dfs优化了不知道多少.(还是91分,不知道剩下那个数据有多毒瘤)
代码2:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| #include<iostream>
#include<queue>
#include<cstring>
#include<algorithm>
#include<fstream>
using namespace std;
int life=10;
int d1[1100][1100],d2[1100][1100];
int n,d;
struct junk{
int h,t,l;
};
int cmp(junk a,junk b)
{
return a.t<b.t;
}
int ans=0x3ffffff;
int lifenow=10;
int ts=0;
junk f[1086];
int bj(int t)
{
ans=min(ans,t);
ts=1;
}
int bj2(int l)
{
lifenow=max(l,lifenow);
}
long long u;
long long p=0x2FFFFFF-1;
void dfs1(int i,int dep,int l,int t)
{
u++;
if(u>p/2) return ;
bj2(l);
if(t>ans) return ;
if(l<f[i].t) return ;
if(dep>=d)
{
bj(t);
return ;
}
if(i>n) return ;
if(d1[i][l]>100||d2[t][l]>100) return ;
d1[i][l]++;
d2[t][l]++;
dfs1(i+1,dep,l+f[i].l,f[i].t);
dfs1(i+1,dep+f[i].h,l,f[i].t);
if(u>p/2) return ;
}
}
int main()
{
cin>>d>>n;
int h=0;
int i,j,k;
for(i=1;i<=n;i++)
cin>>f[i].t>>f[i].l>>f[i].h;
sort(f+1,f+n+1,cmp);
dfs1(1,0,10,0);
if(ts)
cout<<ans;
else cout<<lifenow;
return 0;
}
|
这怪东西是我初中写的,现在看来怪怪也很正常,而且这东西还在19年6月被大佬d过
这个题可以思考的剪枝很多,也比埃及分数这种剪枝也要简单(可惜大部分OIer还是用蛋糕或者埃及分数入门剪枝)
一个怪题

这东西打算怎么做?
分块打表
T1.求小于x的素数的个数
假设x<=109
我们假设遇到了一个叫做cyx的出题人(这名字是我乱打的),他只给你8MB的空间
这东西该怎么办呢?
只有忍受吗
并不是,考虑哪种筛法不需要存数组
显然有两种
一个是n的暴力,另一个是MillerRobin
实际上为了求稳的话你多半连第二种算法想都不想
但是现在cyx说只有10%的数据满足n≤100000
所以你又只有忍受了(
那你现在得想办法怎么优化这个,你想了个办法
把每个素数都打了个表下来
然后发现这数字还真不小大概在2-3W的时候就破了128KB,只好另外想个办法。
瞎搞的时候发现2性质很好用,此时可以想象我们在做一个分块题,[1,n]的质数分为k个块,对于前k-1个块,我们可以通过打表找到答案,然后剩下一个块逐一进行普通的O(N)暴力判断就好了,时间复杂度大概在O(N∗K) 因为N≤10000,时间复杂度在108以内,然后考虑到2性质,这里K取700是比较保险的,时间复杂度很接近108这个上限,但是不会超过,实测能过80分的点。
其实这里面已经用到了分块打表的思想了(隔p隔素数打一个)
然后你就骗到了100分,实际上这题的n到了1011所以你只能拿到80分
悬线法
O(NM)
T1
1.设置 l[i] [j] 表示 (i,j)最左边能拓展到的点。
r[i] [j] 表示 (i,j)最右边能拓展到的点。
up[i] [j] 表示能拓展到的最上面的点。
初始化 l[i] [j] = r[i] [j] = j;
mp[i] [j] 表示地图 (i,j) 的状态 。
up[i] [j] 表示 (i,j) 能向上拓展的最大的高度,把它初始化为1。
然后我们可以轻易的推出预处理公式(我们暂时认为 我们要找最大全是1的正方形)
为了简化问题,我们先来看看矩形
如果左边那个点是1,那么这个点就可以向左边拓展,能拓展的最左边的点=上个点能拓展的最左边的点。
同理,右边也是一样。
1
2
3
4
5
6
7
8
9
10
11
| inline void getlr()
{
register int i,j;
for(i=1;i<=n;i++)
for(j=2;j<=m;j++)
if(mp[i][j]==mp[i][j-1]&&mp[i][j]==1) l[i][j]=l[i][j-1];
for(i=1;i<=n;i++)
for(j=m-1;j>=1;j--)
if(mp[i][j]==mp[i][j+1]&&mp[i][j]==1) r[i][j]=r[i][j+1];
return ;
}
|
现在预处理完毕后,我们枚举每个点 (i,j) 能够轻易得到这个点所在的最大矩形宽度a =(r [i] [j] -l [i] [j] +1)
于是横着的问题就解决了,竖着就是 up [i] [j]
因此它的最大面积就是 a*up[i] [j]
那么怎么转移呢?
如果上一个点是 1,这个点也是1的话,那么我们可以得到这个方程
l[i] [j]=max(l[i] [j],l[i-1] [j]), r[i] [j]=min(r[i] [j],r[i-1] [j]),up[i] [j]=up[i-1] [j]+1
别忘了这是个二维矩阵,i可以理解为高度。
于是代码就有了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| #include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<queue>
#include<map>
#include<set>
#include<vector>
#include<stack>
#include<algorithm>
using namespace std;
int n,m,up[110][110],l[110][110],r[110][110],ans;
int mp[110][110];
inline void getlr()
{
register int i,j;
for(i=1;i<=n;i++)
for(j=2;j<=m;j++)
if(mp[i][j]==mp[i][j-1]&&mp[i][j]==1) l[i][j]=l[i][j-1];
for(i=1;i<=n;i++)
for(j=m-1;j>=1;j--)
if(mp[i][j]==mp[i][j+1]&&mp[i][j]==1) r[i][j]=r[i][j+1];
return ;
}
inline void dp()
{
register int i,j;
for(i=2;i<=n;i++)
for(j=1;j<=m;j++)
{
if(mp[i][j]==mp[i-1][j]&&mp[i][j]==1) l[i][j]=max(l[i][j],l[i-1][j]),r[i][j]=min(r[i][j],r[i-1][j]),up[i][j]=up[i-1][j]+1;
int a,b;
a=r[i][j]-l[i][j]+1;
b=min(a,up[i][j]);
ans=max(ans,b*b);
}
return ;
}
int main()
{
int i,j;
scanf("%d %d",&n,&m);
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
scanf("%d",&mp[i][j]),l[i][j]=r[i][j]=j,up[i][j]=1;
getlr();
dp();
ans=sqrt(ans);
printf("%d",ans);
return 0;
}
|
O(S^2) 做法
S为点数量。
当 N M 极大的时候,上面的nm 做法就会TLE
因此我们有必要学习这个做法。
T2
N,M<=30000
一看就知道不是NM的做法。
S^2的做法很怪,但是可以尽量看下去。
做法很生猛,对于每一个点都来和其他的点比较一下,然后找最大的。
首先排序了一次,让每个点的循环(i)只用对另外每一个点判断一次
设置 l,r,h; 这些东西他们都不是数组了
l,r,h意义和原来差不多。
首先按照高度进行排序
然后 for i,j in [1,s]
然后循环的时候j从i断开。
对于高度比第i小的点单独dp,比他大的单独dp
初始状态 r=m,l=0
对于j<i h=n-q[i].x
对于j>i h=q[i].x
然后比较的时候,r必然向左,l必然向右。
所以得到dp方程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| for(i=1;i<=s;i++)
{
int r=m,l=0,h=n-q[i].x;
for(j=i+1;j<=s;j++)
{
if(h*(r-l)<=ans) break;
ans=max(ans,(q[j].x-q[i].x)*(r-l));
if(q[i].y==q[j].y) break;
if(q[j].y>q[i].y) r=min(r,q[j].y);
if(q[j].y<q[i].y) l=max(l,q[j].y);
}
r=m,l=0,h=q[i].x;
for(j=i-1;j>=1;j--)
{
if(h*(r-l)<=ans) break;
ans=max(ans,(q[i].x-q[j].x)*(r-l));
if(q[i].y==q[j].y) break;
if(q[j].y>q[i].y) r=min(r,q[j].y);
if(q[j].y<q[i].y) l=max(l,q[j].y);
}
}
|
完整代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
| #include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<queue>
#include<map>
#include<set>
#include<vector>
#include<stack>
#include<algorithm>
using namespace std;
int n,m,s;
struct que{
int x,y;
}q[10010];
int cmp1(que a,que b)
{
if(a.x==b.x) return a.y<b.y;
return a.x<b.x;
}
int cmp2(que a,que b)
{
if(a.y==b.y) return a.x<b.x;
return a.y<b.y;
}
int main()
{
int i,j;
scanf("%d %d",&n,&m);
scanf("%d",&s);
for(i=1;i<=s;i++)
{
scanf("%d %d",&q[i].x,&q[i].y);
}
q[++s].x=0;
q[++s].x=n,q[s].y=0;
q[++s].x=0,q[s].y=m;
q[++s].x=n,q[s].y=m;
int ans=0;
sort(q+1,q+s+1,cmp1);
for(i=1;i<=s;i++)
{
int r=m,l=0,h=n-q[i].x;
for(j=i+1;j<=s;j++)
{
if(h*(r-l)<=ans) break;
ans=max(ans,(q[j].x-q[i].x)*(r-l));
if(q[i].y==q[j].y) break;
if(q[j].y>q[i].y) r=min(r,q[j].y);
if(q[j].y<q[i].y) l=max(l,q[j].y);
}
r=m,l=0,h=q[i].x;
for(j=i-1;j>=1;j--)
{
if(h*(r-l)<=ans) break;
ans=max(ans,(q[i].x-q[j].x)*(r-l));
if(q[i].y==q[j].y) break;
if(q[j].y>q[i].y) r=min(r,q[j].y);
if(q[j].y<q[i].y) l=max(l,q[j].y);
}
}
sort(q+1,q+s+1,cmp2);
for(i=1;i<s;i++) ans=max(ans,(q[i+1].y-q[i].y)*n);
printf("%d",ans);
return 0;
}
|
分块
应该都学会了,不过应该都没用过
来一个模板题吧
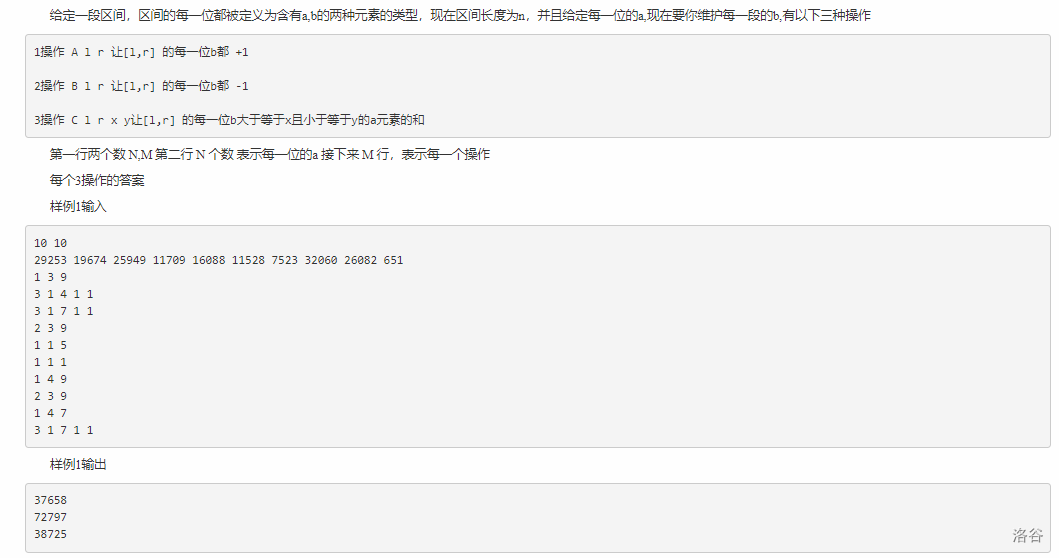
应该都会做吧
*说解法时间
这道题其实就是个分块,数据有的,线段树被我卡了(大概),可以用来打打分块
凸包
首先凸包的定义:
用不严谨的话来讲,给定二维平面上的点集,凸包就是将最外层的点连接起来构成的凸多边形,它能包含点集中所有的点。
(百度百科给的解释)
因此以下就可以算是一个凸包
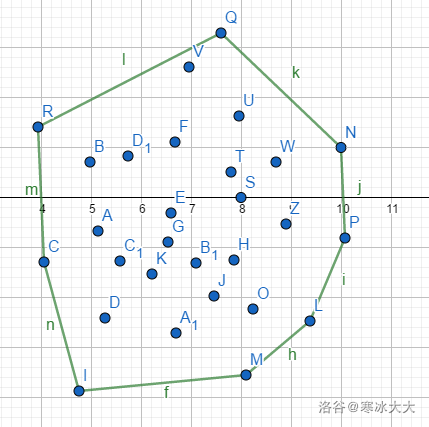
求法有两个
求法 1
第一个是把凸包分为上下两部分,对于下半部分不难发现斜率是在递增的,因此考虑先给所有点按照从左到右从下到上排序,然后类似于单调栈维护一个斜率。
然后伪代码大概就长这样
1
2
3
4
5
| for(i=1;i<=n;i++)
{
s[++size]=p[i];
while(size>=3&&getk(s[size-2],s[size])<getk(s[size-2],s[size-1])) s[size-1]=s[size],size--;
}
|
getk(node a,node b) 是求AB所在直线斜率,特别注意A,B相等的时候返回一个极大值。
对于上半部分凸包,只需要从右向左枚举即可。
求法2
上面的求法不需要高中数学功底因此可见只能解决较简单的问题对于比较毒瘤的问题,这样进一步写下去就很麻烦,所以考虑求法2
Graham扫描法
首先前置芝士
1.极角排序
这里只介绍按照atan2的方法。
atan2(x,y) 即返回tanα=yx 的α同时α∈[−π,π]
例如我们以左下角E(优先考虑最下)点对这些点极角排序,显然可见a
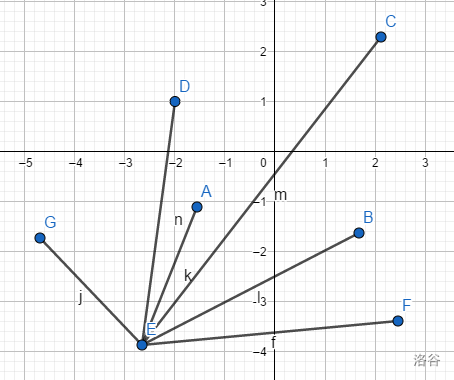
ABCDEFG的坐标:
7
-1.56 -1.11
1.68 -1.63
2.12 2.29
-2 1
-2.66 -3.87
2.46 -3.39
-4.7 -1.73
排序的结果是这样的(FBCADG)可以理解为从0度逆时针扫一圈。

atan2 (x,y)当y=0时,tanα不存在 (即tanx=1)返回 0 但是x=0的时候返回-1
2.叉积
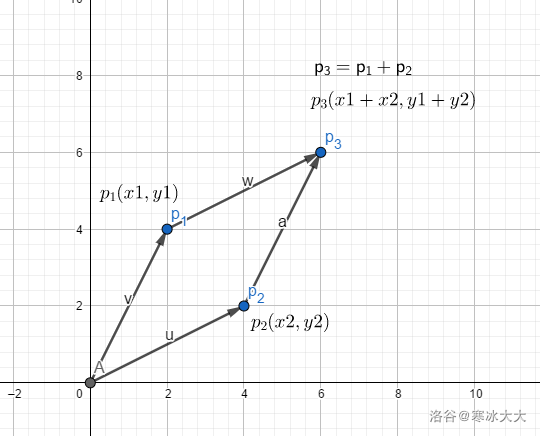
如图所示p1∗p2即为平行四边形面积
公式 p1∗p2=x1y2−x2y1
原理可以参考下面这张出,出处大概在这里,由于图片加载太慢我放在图床上面了

同时四边形面积大于0说明p2在p1顺时针方向,如果==0重合,如果小于0就说明在逆时针方向
算叉积的时候可以用这个公式
(bx−ax)∗(cy−ay)−(by−ay)∗(cx−ax)
=(axby−bxay)+(bxcy−cxby)+(cxay−axcy)
=a∗b +b∗c +c∗a
c如果在a右边的话,c∗a 面积就是小于0的
同理,如果上面的式子大于0,就说明c不在凸包里面。
如下图所示
刚开始d,b在栈里面,此时比较(d,c,b),发现>0则c入栈
同理对于d,比较(b,d,c)也大于0,入栈
运行完毕,发现O→b→c→d→O就是凸包。
对于小于O的情况的解释:
例如 b,c,N三个点,按照极角排序,就是b,c,N,现在我们假设b,c在栈里面,就要比较(b,N,c),此时小于0,即c并不在凸包上(N取代了他的位置)
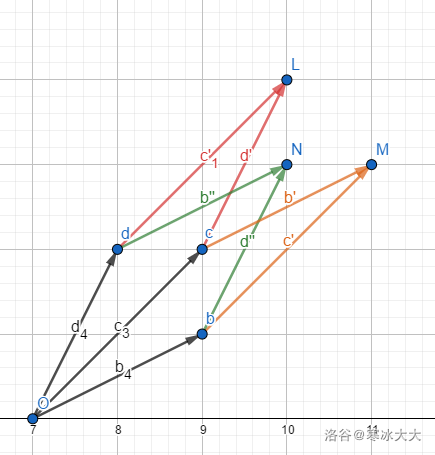
实际上推完了上面的东西,你就能写出来代码了.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
| #include<iostream>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<set>
#include<algorithm>
using namespace std;
const double eps=1e-3;
int n,m,size;
double ans;
struct node{
double x,y;
}p[200200],s[200200];
inline int cmp(node a,node b)
{
double k1,k2;
k1=atan2((a.y-p[1].y),(a.x-p[1].x));
k2=atan2((b.y-p[1].y),(b.x-p[1].x));
if(k1!=k2) return k1<k2;
return a.x<b.x;
}
inline double getdis(node a,node b)
{
return sqrt(1.0*(a.x-b.x)*(a.x-b.x)+1.0*(a.y-b.y)*(a.y-b.y));
}
inline double getcj(node a,node b,node c)
{
return 1ll*(b.x-a.x)*(c.y-a.y)-1ll*(b.y-a.y)*(c.x-a.x);
}
inline int bj(node a,node b)
{
return (a.y>b.y||(a.y==b.y)&&(a.x>b.x));
}
void gettb()
{
p[0].x=p[0].y=0x3f3f3f3f;
register int i,j;
for(i=1;i<=n;i++)
{
if(bj(p[0],p[i])) p[0]=p[i],j=i;
}
swap(p[j],p[1]);
sort(p+2,p+n+1,cmp);
s[++size]=p[1];s[++size]=p[2];
for(i=3;i<=n;)
{
if(size>=2&&getcj(s[size-1],p[i],s[size])>=0) size--;
else s[++size]=p[i++];
}
s[0]=s[size];
for(i=1;i<=size;i++) ans+=getdis(s[i-1],s[i]);
}
int main()
{
register int i,j;
scanf("%d",&n);
for(i=1;i<=n;i++) scanf("%lf %lf",&p[i].x,&p[i].y);
gettb();
printf("%.2lf",ans);
return 0;
}
|
旋转卡壳
旋(xuán)转(zhuàn)卡(qia)壳(qiào)
求凸包的直径一种方法
首先我们求出来一个凸包(绿色),然后才能找直径(红色)(bushi)
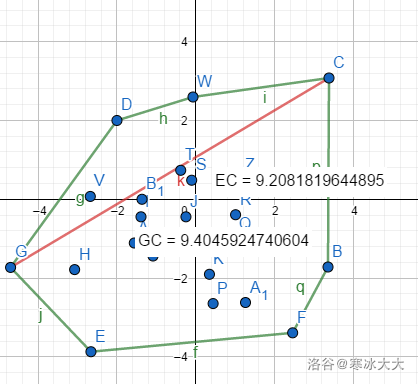
其实只要找到最长距离的两个点就可以了
找直径的方式:找两个点,做一条平行线,然后比较距离~~(其实并没有什么用,但是我们要引入旋转卡壳)~~
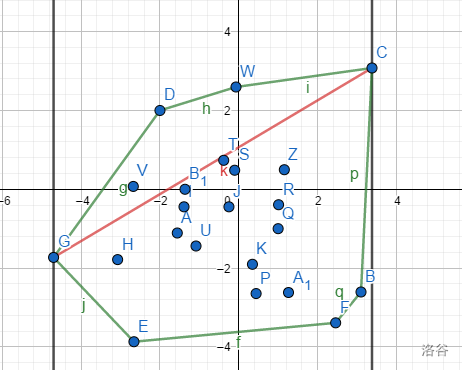
实际上我们可以转化为两个相邻的点的线段所在的直线到最远的点的距离,这样单纯的算距离就变成了求三角形面积。
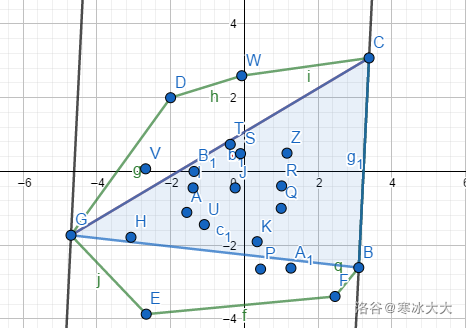
我们在做无用功?
不是,于是精彩的来了,(如下图)CB为底的三角形面积是单峰函数,我们扫描出来了CB为底的最大值,比较GC,GB的距离,然后逆时针上去(E→F→B→...以此类推)
这时候对底边面积最大的点一定在逆时针移动(用手推一推就好了)
这样不难发现三角形的顶点(这里姑且认为是临边不与这条平行线重合的点)不会再回到原来的点。
因此时间复杂度达到了美妙的O(Nlog2N)(排序占了大头)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
| #include<iostream>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<queue>
#include<stack>
#include<vector>
#include<set>
#include<map>
#include<algorithm>
#define int long long
using namespace std;
struct node{
int x,y;
}p[200200],s[200200];
int n,size;
inline int cmp(node a,node b)
{
double k1,k2;
k1=atan2((a.y-p[1].y),(a.x-p[1].x));
k2=atan2((b.y-p[1].y),(b.x-p[1].x));
if(k1==k2) return a.x<b.x;
return k1<k2;
}
inline int getdis(node a,node b)
{
return 1ll*(a.x-b.x)*(a.x-b.x)+1ll*(a.y-b.y)*(a.y-b.y);
}
inline int getcj(node a,node b,node c)
{
return 1ll*(b.x-a.x)*(c.y-a.y)-1ll*(b.y-a.y)*(c.x-a.x);
}
inline int bj(node a,node b)
{
return (a.y>b.y||(a.y==b.y)&&(a.x>b.x));
}
inline void gettb()
{
p[0].x=p[0].y=0x3f3f3f3f;
register int i,j;
for(i=1;i<=n;i++) if(bj(p[0],p[i])) p[0]=p[i],j=i;
swap(p[j],p[1]);
sort(p+2,p+n+1,cmp);
s[++size]=p[1]; s[++size]=p[2];
for(i=3;i<=n;)
{
if(size>=2&&getcj(s[size-1],p[i],s[size])>=0) size--;
else s[++size]=p[i++];
}
s[0]=s[size];
}
inline int getmmx()
{
int ans=0;
if(size==2) return getdis(s[0],s[1]);
int j=2;
for(int i=0;i<size;i++)
{
while(getcj(s[i],s[i+1],s[j])<getcj(s[i],s[i+1],s[j+1])) j=(j+1)%size;
ans=max(ans,max(getdis(s[i],s[j]),getdis(s[i+1],s[j])));
}
return ans;
}
signed main()
{
ios::sync_with_stdio(false);
register int i,j;
cin>>n;
for(i=1;i<=n;i++)
{
cin>>p[i].x>>p[i].y;
}
gettb();
cout<<getmmx()<<endl;
return 0;
}
|
A*
其实这里是一类dfs和搜索方法的总和
包括
A*
IDA*
康拓展开
A* /IDA *
A*
听起来感觉是个高大上的名字?
实际上呢?
就是优先队列+估价函数
首先定义函数: F(x)=G(x)+H(x)
G(x)表示当前的花费,H(x) 表示期望花费。
H(x)相当于是一个剪枝,一定要比实际小,当H(x)=0时,即为普通的爆搜
用一个优先队列把F(x)放进去,取名P
每次取出堆顶,然后把堆顶删除,同时把他丢到A数组里。
显然A里面放进去的必须是更行完成的
然后搜索上下所有四格:
已经在A里面的,不管。
不在P里面的,加进来。
已经在P里的,判断一下是否更优,更新。貌似没用
没用?那你SPFA白学了
G(x)在dfs中更新
H(x)需要预处理
IDA*
迭代加深应该都知道
现在我们遇到了一个CXY的出题人(这名字乱打的)
他想要钓鱼,比如答案在dfs的第二层就有了,但是这个dfs树他给你搞成100000000000层
怎么办呢?
这时候就要迭代加深+A了
说句实话IDA比A *还好理解,除非那种层数特别大的(值得答案层数,比如一张图)一般都用的IDA *
思想大概懂了,所以来说说细节
怎样找到比较好的H(x)呢
F一般是当状态离目标越近时越优,不过有例外
估值函数里的参数一般是比较明显的,且每次操作后一般会改变的,一般也会满足上面这个。
参数一般变化是有范围的
例题
有一个象棋棋盘,上面有一个空格和很多个红色的马和白色的马,每个马都可以走到空格,问要走多少步才让这个棋盘到达目标状态(题目给出)
现在我们假设棋盘大小5*5,保证答案不超过15
cdq分治
这东西有点难讲啊(
那就讲讲偏序问题吧
偏序问题
总的说来,解决问题的方法很多
一维偏序:
二维偏序:
- 运用排序解决一维,然后变成一维偏序
- 主席树
- 二维树状数组(一般不会有人写)
- K-D tree,有根号(便于理解不过一般不会有人写)
三维偏序:
- CDQ分治
- 用二维偏序假装成三位偏序骗你打CDQ的出题人
更高维的一般不会有人出了,因为复杂度已经很接近n2或者比n2高了
cdq
现在我们就来说说二维偏序问题
也就是逆序对
cdq分治的思想就是把一个区间[l,r]分成[l,mid],[mid+1,r](就像线段树)
然后我们cdq合并的时候只需要处理左端点在左半部分右端点在右半部分的情况了。
因为我们认为在之前的分治中,[l,mid]已经被更下面的分治处理完了。
显然这东西处理的顺序和线段树都一样,因此这东西就是NlogN的复杂度
可能你会问那这个东西有啥用
你想一想树套树不浪费空间吗
上面这个感性理解就可以了,其实我想讲三维偏序
三位偏序顾名思义就是加了另一个维度
这个时候我们就可以树套树了
出题人稍微卡卡空间就只有忍受了
所以我们得用cdq
啥意思呢,我们按照cdq分治的顺序,然后将一个三位偏序的大问题转换成nlogn个子问题
那么cdq怎么用呢,我们用三位偏序的模板为例
由于左右端点在一个区间内的情况已经处理完了,我们只要处理不在一个端点的
代码就这样了,自己看吧
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| void cdq(int l,int r)
{
if(l==r) return ;
int mid=(l+r)>>1;
cdq(lson);
int i=l,j=mid+1;
while(j<=r&&i<=mid)
{
while(a[i].b<=a[j].b&&i<=mid)
{
ct.add(a[i].c,a[i].sz);
i++;
}
a[j].ans+=ct.getsum(a[j].c);
debug[j]=a[j].ans;
}
for(j=l;j<=i-1;j++) ct.add(a[j].c,-a[j].sz);
sort(a+l+1,a+r+1);
cdq(rson);
}
|
康康多少人离线了
好了告诉你们上面这段代码是错的
问题是上面这个代码错了几个
来找一找~~(拖时间)~~
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| void cdq(int l,int r)
{
if(l==r) return ;
int mid=(l+r)>>1;
cdq(lson); cdq(rson);
int i=l,j=mid+1;
while(j<=r)
{
while(a[i].b<=a[j].b&&i<=mid)
{
ct.add(a[i].c,a[i].sz);
i++;
}
a[j].ans+=ct.getsum(a[j].c);
debug[j]=a[j].ans;
j++;
}
for(j=l;j<=i-1;j++) ct.add(a[j].c,-a[j].sz);
sort(a+l,a+r+1);
}
|
模拟退火
这东西也有点难讲啊
模拟上火
模拟上火的兄弟
dp 水分
上下界的网络流
题目&题解
杂题
T1 P1156 垃圾陷阱
P6025 线段树
分块打表
T1

悬线法
2.P1387 最大正方形
3.P1578 奶牛浴场
凸包
T1 模板题
旋转卡壳
T1 旋转卡壳模板
cdq分治
P3810 【模板】三维偏序(陌上花开
A*
P2324 [SCOI2005]骑士精神
拓展阅读

















