呜呼呼呼呼呼呼呼

FFT

只说FFT在优化多项式乘法的应用。

首先我们有两个系数表达的多项式f,gf,g

f(x)=a1xk+a2xk−1....akx+ak+1f(x)=a_1x^k+a_2x^{k-1}....a_{k}x+a_{k+1}

g(x)=a1xp+a2xp−1....apx+ap+1g(x)=a_1x^p+a_2x^{p-1}....a_{p}x+a_{p+1}

现在我们要求得F=f∗gF=f*g

显然我们可以爆算，时间复杂度O(n2)O(n^2)

然而对nn较大的时候，上面显然超时，所以我们就得学习一个更优秀的解决问题的办法:FFT

FFT的具体思路：先把系数表达转换成点值表达，然后可以O(n)O(n)地把点值表示相乘，最后通过IDFT转化回系数表达

前置芝士

下面这一部分其实可以跳过，不会讲FFT具体操作

点值表示

就是用n+1n+1个点来表示一个多项式

至于为啥是n+1n+1，我们有n+1n+1个未知数，为了得到唯一解必须要这么多。

虚数

形如a+bia+bi的数，其中a,ba,b是实数，且b≠0,i2=−1b\neq0,i^2=-1。

在FFT中我们需要这三个运算

假设x,yx,y是虚数其中x=a+bi,y=c+dix=a+bi,y=c+di

x+y=(a+c)+(b+d)ix+y=(a+c)+(b+d)i

x−y=(a−c)+(b−d)ix-y=(a-c)+(b-d)i

x∗y=(ac−bd)+(ad+bc)ix*y=(ac-bd)+(ad+bc)i

欧拉公式

eix=cosx+isinxe^{ix}=cosx+isinx

单位负根

就是xn=1x^n=1的解

就是在坐标系上把r=1r=1的圆均分成nn份，比如这是当n=4n=4时候的情况

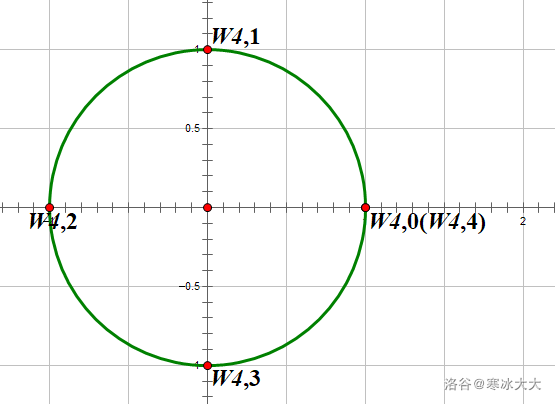
他有啥性质

wnn=1w^{n}_{n}=1

wnk=w2n2kw_{n}^{k}=w_{2n}^{2k}

w2nk+n=−w2nkw_{2n}^{k+n}=-w_{2n}^{k}

具体操作

系数表示转化成点值表示

这也叫作DFT

现在我们又一个多项式

f(x)=a7x7+a6x6+a5x5+a4x4+a3x3+a2x2+a1x+a0f(x)=a_7x^7+a_6x^6+a_5x^5+a_4x^4+a_3x^3+a_2x^2+a_1x+a_0

如果我们硬求n+1n+1个点出来，复杂度是O(n2)O(n^2)的

这时候就有一个很巧妙的东西了，我们把奇数项和偶数项单独提出来

f(x)=a6x6+a4x4+a2x2+a0+a7x7+a5x5+a3x3+a1xf(x)=a_6x^6+a_4x^4+a_2x^2+a_0+a_7x^7+a_5x^5+a_3x^3+a_1x

f(x)=a6x6+a4x4+a2x2+a0+x(a7x6+a5x4+a3x2+a1)f(x)=a_6x^6+a_4x^4+a_2x^2+a_0+x(a_7x^6+a_5x^4+a_3x^2+a_1)

然后令g,hg,h

g(x)=a6x3+a4x2+a2x1+a0g(x)=a_6x^3+a_4x^2+a_2x^1+a_0

h(x)=a7x3+a5x2+a3x1+a1h(x)=a_7x^3+a_5x^2+a_3x^1+a_1

那么有f(x)=g(x2)+xh(x2)f(x)=g(x^2)+xh(x^2)

然而这还不够，根据单位复根

w2nk=−w2nk+nw_{2n}^k=-w_{2n}^{k+n}

那么有f(w2nk+n)=g((w2nk)2)−w2nkh((w2nk)2f(w_{2n}^{k+n})=g({(w_{2n}^{k})}^2)-w_{2n}^{k}h({(w_{2n}^{k})}^2

因此我们每次可以只算前一半的值，然后可以根据这个公式得到后一半的值

通过分治，可以时间复杂度变为O(nlogn)O(nlogn)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

struct comp{
	double a,b;
	comp(double aa=0,double bb=0){a=aa; b=bb;}
}a[maxn],b[maxn];

comp operator +(const comp a,const comp b){return comp(a.a+b.a,a.b+b.b);}
comp operator -(const comp a,const comp b){return comp(a.a-b.a,a.b-b.b);}
comp operator *(const comp a,const comp b){return comp(a.a*b.a-a.b*b.b,a.a*b.b+a.b*b.a);}

void fft(int len,comp *a)
{
	if(len==1) return ;
	comp a1[(len>>1)+1],a2[(len>>1)+1];
	int i;
	for(i=0;i<=len;i+=2) a1[i>>1]=a[i],a2[i>>1]=a[i+1];
	fft(len/2,a1); fft(len/2,a2);
	comp w=comp(1,0); comp k=comp(cos(pi*2.0/len),sin(pi*2.0/len));
	for(i=0;i<len/2;i++,w=w*k) a[i]=a1[i]+w*a2[i],a[i+len/2]=a1[i]-w*a2[i];
}

点值表示转化成系数表示

这也叫做IDFT

现在我们算出来很多yy的值，如果单纯来解方程的话，时间复杂度n3{n^3}原地爆炸

这里先说公式

离散傅里叶变换

bk=∑i=0n−1ai∗wnkib_k=\sum_{i=0}^{n-1}\limits a_i*w_{n}^{ki}

离散傅里叶逆变换

ak=1n∑i=0n−1bi∗wn−kia_k=\frac{1}{n}\sum_{i=0}^{n-1}\limits b_i*w_n^{-ki}

证明:

首先我们单纯地把bib_i带入,同时约去1n\frac{1}{n}

\begin{eqnarray} \sum_{i=0}^{n-1}\limits b_iw_n^{-ki} &=& \sum_{i=0}^{n-1}\limits w_{n}^{-ki} \sum_{j=0}^{n-1}\limits w_{n}^{ij}a_j\\ & =& \sum^{n-1}_{j=0}a_j\sum^{n-1}_{i=0}w_n^{-ki}*w_n^{ij} \\ & =& \sum^{n-1}_{j=0}a_j\sum^{n-1}_{i=0} w_n^{i(j-k)} \end{eqnarray}

考虑∑i=0n−1wni(j−k)\sum^{n-1}_{i=0}\limits w_n^{i(j-k)}

如果j=kj=k 那么显然的原式=n=n

否则这就是个公比为wn(j−k)w_n^{(j-k)}的等比数列，考虑求和

那么就有s=a1∗1−qn1−qs=a1* \frac{1-q^n}{1-q}显然a1=1a1=1

说明

(wnj−k)n=(wnn)j−k=1=qn({w_n^{j-k}})^n=({w_n^{n}})^{j-k}=1=q^n

那么s=0s=0

原式就变成了

\begin{eqnarray} \frac{1}{n}\sum_{i=0}^{n-1}\limits b_iw_n^{-ki}&=&\frac{1}{n}\sum^{n-1}\limits_{j=0}a_j\sum^{n-1}_{i=0} \limits w_n^{i(j-k)} \\ &=& \frac{1}{n} \sum^{n-1}_{j=0}a_j\sum^{n-1}_{i=0} w_n^{i(j-k)} \\ &=& \frac{1}{n}*n*a_k\\&=&a_k \end{eqnarray}

因此得证

这东西有啥用

我们发现除了分母又一个1n\frac{1}{n}和wnw_n上面有个负号外其他的都和DFT一样,因此我们考虑用上面那个代码，传一个−1-1的参数，然后做完了最后除nn就是我们想要的系数了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

void fft(int len,comp *a,int t)
{
	if(len==1) return ;
	comp a1[(len>>1)+1],a2[(len>>1)+1];
	int i;
	for(i=0;i<=len;i+=2) a1[i>>1]=a[i],a2[i>>1]=a[i+1];
	fft(len/2,a1,t); fft(len/2,a2,t);
	comp w=comp(1,0); comp k=comp(cos(pi*2.0/len),t*sin(pi*2.0/len));
	for(i=0;i<len/2;i++,w=w*k) a[i]=a1[i]+w*a2[i],a[i+len/2]=a1[i]-w*a2[i];
}

//最后输出的时候
for(i=0;i<=n+m;i++) cout<<int(a[i].a/lmt+0.49)<<" ";

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include<stdio.h>
#include<iostream>
#include<cmath>
#include<cstring>
#include<queue>
#include<stack>
#include<vector>
#include<set>
#include<map>
#include<algorithm>

using namespace std;

const int maxn=4201000;
const double pi=3.1415926535897932;
int n,m,lmt=1;

struct comp{
	double a,b;
	comp(double sa=0,double sb=0){a=sa; b=sb;}
}a[maxn],b[maxn];

comp operator +(const comp a,const comp b){return comp(a.a+b.a,a.b+b.b);}
comp operator -(const comp a,const comp b){return comp(a.a-b.a,a.b-b.b);}
comp operator *(const comp a,const comp b){return comp(a.a*b.a-a.b*b.b,a.a*b.b+a.b*b.a);}


void fft(int len,comp *a,int t)
{
	if(len==1) return ;
	comp a1[(len>>1)+1],a2[(len>>1)+1];
	int i;
	for(i=0;i<=len;i+=2) a1[i>>1]=a[i],a2[i>>1]=a[i+1];
	fft(len/2,a1,t); fft(len/2,a2,t);
	comp w=comp(1,0); comp k=comp(cos(pi*2.0/len),t*sin(pi*2.0/len));
	for(i=0;i<len/2;i++,w=w*k) a[i]=a1[i]+w*a2[i],a[i+len/2]=a1[i]-w*a2[i];
}

int main()
{
	ios::sync_with_stdio(false);
	register int i,j;
	cin>>n>>m;
	for(i=0;i<=n;i++) cin>>a[i].a;
	for(i=0;i<=m;i++) cin>>b[i].a;
	while(lmt<=(n+m)) lmt*=2
	fft(lmt,a,1); fft(lmt,b,1);
	for(i=0;i<=lmt;i++) a[i]=a[i]*b[i];
	fft(lmt,a,-1);
	for(i=0;i<=n+m;i++) cout<<int(a[i].a/lmt+0.49)<<" ";
	cout<<endl;
	return 0;
}

优化

首先我们手工推一下FFT过程

1
2
3
0 1 2 3 4 5 6 7
0 2 4 6 1 3 5 7 
0 4 2 6 1 5 3 7

观察到每行的差值不一样（废话）

然后第一行的二进制是这样的

1
2
3
000 001 010 011 100 101 110 111
000 010 100 110 001 011 101 111
000 100 010 110 001 101 001 111

发现第一层和最后一层就像是翻转了，实际上就是这样，证明没那个必要，那我们就可以在FFT之前得到这个数组，然后FFT就不需要递归进行了

因为它的分治过程

1
2
3
0 4 2 6 1 5 3 7 
0 2 4 6 1 3 5 7 
0 4 2 6 1 5 3 7

每一层FFT的时候，都是左边*右边，因此结果是一样的

所以不需要复制，我们考虑一下怎么构造这个数组

由于是从小到大枚举，我们理所应当地认为i/2i/2已经处理好了（除了0，但是不用管，因此我们得到了i/2i/2的翻转值，由于我们,这里是整数除法），然后还需要向右移一位，一是因为那一位没有用，而是我们还有一最后一个二进制位没有翻转

1
for(i=0;i<lmt;i++) pla[i]=(pla[i>>1]>>1)|((i&1)?lmt>>1:0);

还有一些其他的优化，但是提升远没有这个明显（除了三次变两次优化）

整个代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include<iostream>
#include<cmath>
#include<stdio.h>
#include<cstring>
#include<queue>
#include<stack>
#include<vector>
#include<set>
#include<map>
#include<algorithm>

using namespace std;

const int maxn=2100010;
const double pi=3.1415926535897;
int n,m,lmt;
int pla[maxn];

struct comp{
	double x,y;
	comp(double xx=0,double yy=0) {x=xx;y=yy;}
}a[maxn],b[maxn];

comp operator +(const comp &a,const comp &b){return comp(a.x+b.x,a.y+b.y);}
comp operator -(const comp &a,const comp &b){return comp(a.x-b.x,a.y-b.y);}
comp operator *(const comp &a,const comp &b){return comp(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}

void fft(comp *a,int t)
{
	int i,j,len,p;
	for(i=0;i<lmt;i++) if(i<pla[i]) swap(a[i],a[pla[i]]);
	for(p=2;p<=lmt;p<<=1)
	{
		len=p>>1;
		comp k=comp(cos(2.0*pi/p),1.0*t*sin(2.0*pi/p));
		for(i=0;i<lmt;i+=p)
		{
			comp w=comp(1,0);
			for(j=i;j<i+len;j++)
			{
				comp looker=a[j+len]*w;
				a[j+len]=a[j]-looker;
				a[j]=a[j]+looker;
				w=w*k;
			}
		}
	}
}

int main()
{
	ios::sync_with_stdio(false);
	register int i,j;
	cin>>n>>m;
	for(i=0;i<=n;i++) cin>>a[i].x;
	for(i=0;i<=m;i++) cin>>b[i].x;
	lmt=1;
	while(lmt<=(n+m)) lmt<<=1;
	for(i=0;i<lmt;i++) pla[i]=(pla[i>>1]>>1)|((i&1)?lmt>>1:0);
	fft(a,1); fft(b,1);
	for(i=0;i<lmt;i++) a[i]=a[i]*b[i];
	fft(a,-1);
	for(i=0;i<=n+m;i++) cout<<int((a[i].x)/lmt+0.49)<<" ";
	cout<<endl;
	return 0;
}

NTT

前置芝士

原根

原根有这个东西

(a,m)=1(a,m)=1使$a^l \equiv 1(\mod m) 成立的最小的成立的最小的l就是就是a关于模关于模m的阶，记做的阶，记做ord_ma$

如果∃(g,m)=1\exist (g,m)=1并且ordmg=ϕ(m)ord_mg=\phi(m)那么就说明gg是mm的一个原根

此时{g,g2,...,gϕ(m)}\{g,g^2,...,g^{\phi(m)}\}构成了一个模mm的既约剩余系

那他有啥意义，当我们取一个质数的时候ϕ(m)=m−1\phi(m)=m-1

这个时候就具有了单位复根的性质

而且空间相较于FFT少了一半，同时也变成了整数乘法不会损失

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include<iostream>
#include<cmath>
#include<stdio.h>
#include<cstring>
#include<queue>
#include<stack>
#include<vector>
#include<set>
#include<map>
#include<algorithm>

#define int long long

using namespace std;

const int maxn=2100100;
const int modp=998244353;

int n,m,a[maxn],b[maxn];
int pla[maxn];
int lmt=1;

inline int ksm(int xx,int y)
{
	long long x=1ll*xx;
	long long ans=1ll;
	while(y)
	{
		if(y&1) ans=(ans*x)%modp;
		x=(x*x)%modp;
		y>>=1;
	}
	return ans%modp;
}

inline void ntt(int *a,int t)
{
	int i,len,p,j;
	for(i=0;i<lmt;i++) if(i<pla[i]) swap(a[i],a[pla[i]]);
	for(p=2;p<=lmt;p<<=1)
	{
		len=p>>1;
		int k=ksm(t,(modp-1)/p);
		for(i=0;i<lmt;i+=p)
		{
			int w=1; 
			for(j=i;j<i+len;j++)
			{
				int looker=(w*a[j+len])%modp;
				a[j+len]=(a[j]-looker+modp)%modp;
				a[j]=(a[j]+looker)%modp;
				w=(w*k)%modp;
			}
		}
	}
}

signed main()
{
	ios::sync_with_stdio(false);
	register int i,j;
	cin>>n>>m;
	for(i=0;i<=n;i++) cin>>a[i];
	for(i=0;i<=m;i++) cin>>b[i];
	while(lmt<=(n+m)) lmt<<=1;
	for(i=0;i<lmt;i++) pla[i]=(pla[i>>1]>>1)|((i&1)?lmt>>1:0);
	ntt(a,3); ntt(b,3);
	for(i=0;i<lmt;i++) a[i]=(1ll*a[i]*b[i])%modp;
	ntt(a,ksm(3,modp-2));
	lmt=ksm(lmt,modp-2);
	for(i=0;i<=n+m;i++) cout<<(a[i]*lmt)%modp<<" ";
	cout<<endl;
	return 0;
}

优化

预处理原根和原根的逆元的1<<p1<<p次方