无源汇上下界可行流
首先保证最小流量
设每个点 δ(t)=f(N+(t),t)−f(N−(t),t)
然后每条边的流量 flownew=flowmax−flowmin
此时若 δ(t)<0 表示 t 流出不足,因此它的出边要增加流量,连一条 t,T 的边,容量为δ(t)
若$ \delta(t)=0$ 流量守恒,不管
若δ(t)>0 那么说明流出过多,因此要增加入邻域的流量,连一条S,T 的边
若 S 到 T 满流,说明可以实现流量平衡
为什么可行呢,一个点不可能同时和 S,T 相连,并且与 S,T 相连的边都可以2实现并且我们在新图已经忽略这些边带来的贡献(必然贡献进入答案),因此在新图中需要增加一些边的流量才能实现这这张图的流量平衡,而判断流量平衡的只需要满足这些不满足流量平衡的点(与 S,T 相连 )平衡(即 S,T 满流) 即可。
有源汇上下界可行流
连接 T,S 变为无源汇即可
有源汇上下界最大流
首先求得可行流,接着在残量网络上面跑一次最大流即可。
这个结论很显然了(
有源汇上下界最小流
考虑刚才的那个过程,我们找到的是符合我们贪心地构造得到的最小流,在满足边流量符合条件的前提下,如果不是最优就说明存在两个点 u,v 满足f(u,v)>0&&f(v,u)>0 因此从 T 跑一遍最大流减去即可。
P5192 Zoj3229 Shoot the Bullet|东方文花帖|【模板】有源汇上下界最大流
有源汇的上下界网络流,这题难的地方是建图而不是上下界网络流
首先考虑状态,把每一天和每个少女作为一个点放在图中。
每天的 Ck 个少女中拍照的个数都在闭区间 Lki,Rki 中,显然是每天对这个点连一个 Rki−Lki 的边
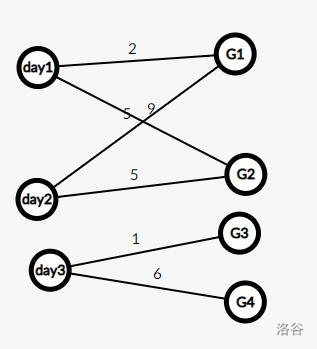
每个少女至少拍摄 Gi 张,因此加一个汇点,连一个 +∞ 的边
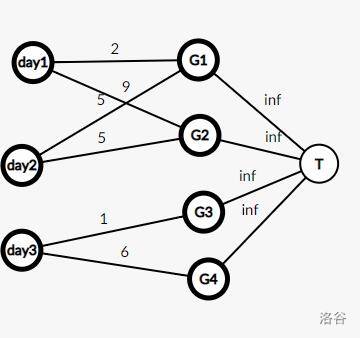
此时还要考虑每天的限制(就是加一个源点,图就不画了)
然后图就减出来了我又老又笨不知道为啥给每天裂点了
然后就按照上面讲的做法做了,注意最后跑s,t 的时候要删边
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
| #include<stdio.h>
#include<iostream>
#include<cmath>
#include<cstring>
#include<queue>
#include<stack>
#include<vector>
#include<set>
#include<map>
#include<algorithm>
using namespace std;
const int maxn=100100;
int n,m,head[maxn],st,ed,_st,_ed,g[maxn],d[maxn],_delta[maxn],cnt[maxn];
int mmf[maxn];
int size=1,dep[maxn],vis[maxn];
int looker;
int c[maxn];
struct edge{
int next,to,flow;
}e[maxn<<1];
inline void addedge(int next,int to,int flow)
{
e[++size].to=to;
e[size].flow=flow;
e[size].next=head[next];
head[next]=size;
e[++size].to=next;
e[size].flow=0;
e[size].next=head[to];
head[to]=size;
}
inline int bfs()
{
queue <int> q;
memset(vis,0,sizeof(vis));
memset(dep,0,sizeof(dep));
q.push(st);
dep[st]=1,vis[st]=1;
while(!q.empty())
{
int t=q.front();
q.pop();
int i,j,k;
for(i=head[t];i;i=e[i].next)
{
j=e[i].to;
k=e[i].flow;
if(k<=0||dep[j]||vis[j]) continue;
vis[j]=1,dep[j]=dep[t]+1;
q.push(j);
}
}
return vis[ed];
}
int dinic(int t,int nowt)
{
if(t==ed||!nowt) return nowt;
int tot=0,j,k,f;
for(int &i=cnt[t];i;i=e[i].next)
{
j=e[i].to;
k=e[i].flow;
if(k>0&&dep[t]+1==dep[j])
{
f=dinic(j,min(nowt-tot,k));
e[i].flow-=f;
e[i^1].flow+=f;
tot+=f;
if(tot==nowt) return tot;
}
}
return tot;
}
inline int getflow()
{
int ans=0;
while(bfs())
{
memcpy(cnt,head,sizeof(cnt));
ans+=dinic(st,0x3f3f3f3f);
}
return ans;
}
inline void solve()
{
int i,j;
st=n+n+m+4,ed=n+n+m+5;
_st=0,_ed=n+n+m+1;
int tmp;
for(i=1;i<=m;i++) cin>>mmf[i],_delta[_ed]-=mmf[i],_delta[n+n+i]+=mmf[i],addedge(n+n+i,_ed,0x3f3f3f3f);
for(i=1;i<=n;i++)
{
cin>>c[i]>>d[i],addedge(_st,i,d[i]);
addedge(i,i+n,d[i]);
int t1,t2,t3;
for(j=1;j<=c[i];j++)
{
cin>>t1>>t2>>t3;
t1++;
addedge(i+n,n+n+t1,t3-t2);
_delta[n+n+t1]-=t2;
_delta[n+i]+=t2;
}
}
for(i=0;i<=n+n+m+1;i++)
{
if(_delta[i]==0) continue;
if(_delta[i]<0) addedge(st,i,-_delta[i]);
if(_delta[i]>0) addedge(i,ed,_delta[i]),looker+=_delta[i];
}
addedge(_ed,_st,0x3f3f3f3f);
int lok=getflow();
if(lok!=looker)
{
cout<<"-1\n\n";
return ;
}
st=_st,ed=_ed;
head[st]=e[head[st]].next;
head[ed]=e[head[ed]].next;
lok+=getflow();
cout<<lok<<"\n\n";
}
inline void memclr()
{
memset(_delta,0,sizeof(_delta));
memset(head,0,sizeof(head));
size=1;
looker=0;
}
int main()
{
ios::sync_with_stdio(false);
while(cin>>n>>m)
{
memclr();
solve();
}
return 0;
}
|







