ER 网络
由 wiki 上面的说法,存在两种 ER 网络,分别为 G(n,p) 与 G(n,M)
G(n,p)
每个点对按照 p 的概率连接
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| void ernp()
{
cin>>n>>p;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
double k=1.0*rand()/RAND_MAX;
if(k<=p)
{
a[i][j]=1;
a[j][i]=1;
m++;
}
}
cout<<n<<" "<<m<<'\n';
for(int i=1;i<=n;i++) cout<<i<<'\n';
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
{
if(a[i][j]) cout<<i<<" "<<j<<'\n';
}
}
|
G(n,M)
随机 n 条边
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| void ernm()
{
cin>>n>>m;
cout<<n<<" "<<m<<'\n';
for(int i=1;i<=m;)
{
int x=rand()%n+1;
int y=rand()%n+1;
if(a[x][y]||x==y) continue;
a[x][y]=a[y][x]=1;
cout<<x<<' '<<y<<'\n';
i++;
}
}
|
但是以上反映出了一个问题,我在 G(n,p) 中考虑到了自环和重边,第二个却没考虑,虽然我也不知道哪个是对的。
UPD: 应该不能有重边和自环。
完整代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| #include<bits/stdc++.h>
using namespace std;
const int maxn=3030;
int n,m,a[maxn][maxn];
double p;
void ernp()
{
cin>>n>>p;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
double k=1.0*rand()/RAND_MAX;
if(k<=p)
{
a[i][j]=1;
a[j][i]=1;
m++;
}
}
cout<<n<<" "<<m<<'\n';
for(int i=1;i<=n;i++) cout<<i<<'\n';
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
{
if(a[i][j]) cout<<i<<" "<<j<<'\n';
}
}
void ernm()
{
cin>>n>>m;
cout<<n<<" "<<m<<'\n';
for(int i=1;i<=m;)
{
int x=rand()%n+1;
int y=rand()%n+1;
if(a[x][y]||x==y) continue;
a[x][y]=a[y][x]=1;
cout<<x<<' '<<y<<'\n';
i++;
}
}
int main()
{
freopen("erg.out","w",stdout);
ios::sync_with_stdio(false);
srand(time(0));
ernp();
}
|
小世界网络
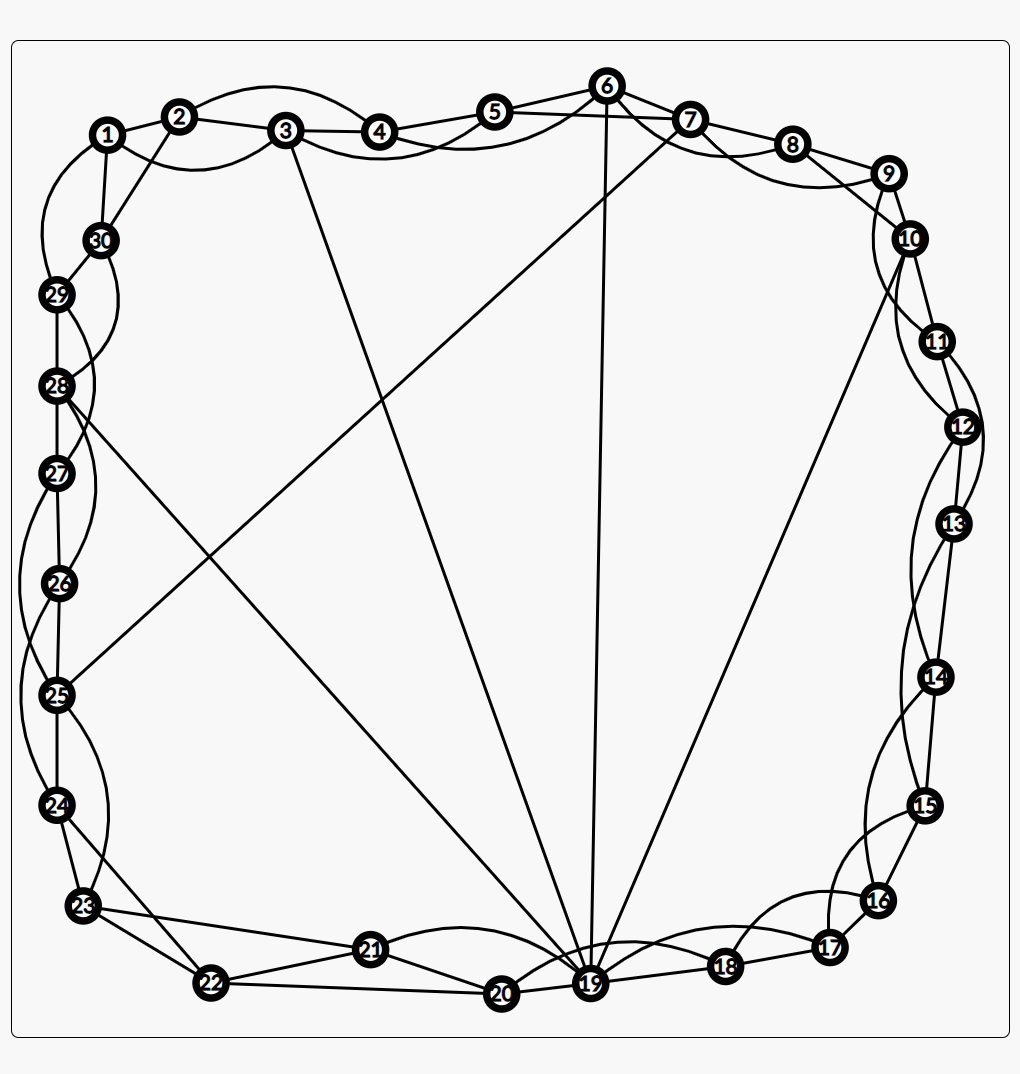
每个点与其周围K个点相连,并且这些边中每条边有 $ p $ 的概率重连(一个端点不变,另一个指向另外一个点,注意没有重边和自环)
尝试用了下茅台19937生成,但是小世界网络具体的定义我没搞太清楚,所以就按照先生成所有的边,然后对每个边进行 p 的概率重连
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| void g_wsn(int n,int k,double p)
{
mt19937 rng(time(0));
int m=n*k/2;
for(int i=1;i<=n;i++)
{
int place=i+1,tmp=k/2;
place=i+1>n?1:i+1;
while(tmp--)
{
a[place][i]=a[i][place]=1;
place=place+1>n?1:place+1;
}
place=i-1>0?i-1:n;
tmp=k/2;
while(tmp--)
{
a[place][i]=a[i][place]=1;
place=place-1>0?place-1:n;
}
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
if(a[i][j]==1)
{
unsigned int tmp=rng();
double lk=pow(2,32);
double ttmp=tmp*1.0/lk;
if(ttmp<p)
{
a[i][j]=a[j][i]=-1;
int target=1ll*rng()%n+1;
while(target==i||a[i][target]==1||target==j) target=1ll*rng()%n+1;
a[target][i]=a[i][target]=2;
}
}
}
cout<<n<<" "<<m<<endl;
for(int i=1;i<=n;i++) cout<<i<<"\n";
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
{
if(a[i][j]>=1) cout<<i<<" "<<j<<'\n';
}
return ;
}
|
无尺度网络
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
| #include<bits/stdc++.h>
using namespace std;
const int maxn=2020;
int n,e0,n0,a[maxn][maxn];
int t,m,N,M;
int deg[maxn*2];
struct mmm
{
int bh,deg;
bool operator <(const mmm &b)
{
if(deg==b.deg) return bh>b.bh;
return deg>b.deg;
}
}b[maxn];
int check(int x)
{
for(int i=1;i<=N;i++)
{
if(x-b[i].deg>=1) x-=b[i].deg;
else return b[i].bh;
}
return 0;
}
void ba_n(int n0,int e0,int t,int m)
{
N=n0,M=e0;
mt19937 rnd(time(0));
for(int i=1;i<=e0;i++)
{
int x,y;
x=rnd()%N+1;
y=rnd()%N+1;
while(x==y||a[x][y])
{
x=rnd()%N+1;
y=rnd()%N+1;
}
a[x][y]=1,a[y][x]=1;
deg[y]++,deg[x]++;
}
for(int i=1;i<=t;i++)
{
for(int j=1;j<=N;j++)
{
b[j].bh=j;
b[j].deg=deg[j];
}
sort(b+1,b+N+1);
map <int,int> mp;
vector <int> v;
for(int j=1;j<=m;)
{
int tmp=rnd()%(2*M)+1;
int x=check(tmp);
if(mp[x]) continue;
v.push_back(x);
mp[x]=1;
j++;
}
for(auto p : v)
{
deg[p]++;
a[p][N+1]++;
a[N+1][p]++;
}
deg[N+1]=m;
N++;
M+=m;
}
cout<<N<<" "<<M<<'\n';
for(int i=1;i<=N;i++) cout<<i<<"\n";
for(int i=1;i<=N;i++)
for(int j=i+1;j<=N;j++)
{
if(a[i][j]) cout<<i<<" "<<j<<"\n";
}
}
int main()
{
freopen("ba_network.out","w",stdout);
ios::sync_with_stdio(false);
cin>>n0>>e0>>t>>m;
ba_n(n0,e0,t,m);
}
|





