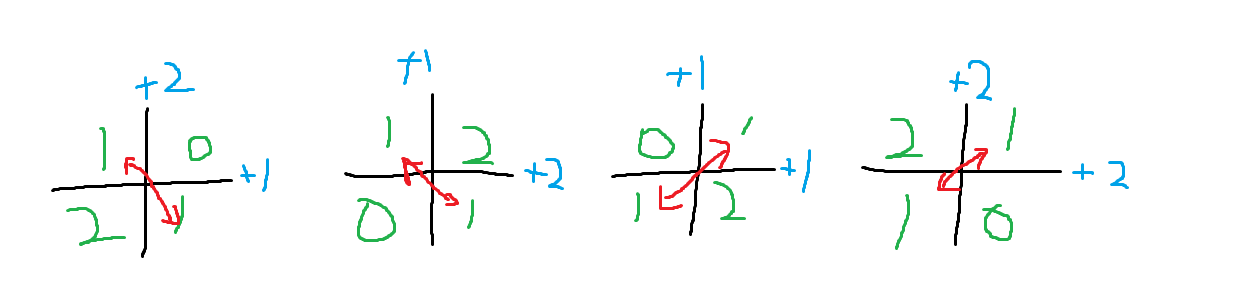管用时间：2023-7.9-2023.7.16

由于有动物学实习，不知道能做多少。

本期主要刷 cf1600-2000 的题目来康复，期望能 div2 做出来

20230711

CF1844A

输出 A+BA+B 即可

CF1844B

把 11 放在最中间，2,32,3 放在最边上即可。

CF1844C

由于可以去除两端而无影响，直接一个 dp 就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<bits/stdc++.h>

#define int long long

using namespace std;

const int maxn=200200;
const int looker=-1e18;

int n,T,f[maxn],ans,a[maxn];

signed main()
{
    ios::sync_with_stdio(false);
    cin>>T;
    while(T--)
    {
        cin>>n;
        for(int i=1;i<=n;i++) cin>>a[i];
        for(int i=0;i<=n;i++) f[i]=looker;
        ans=looker;
        for(int i=1;i<=n;i++)
        {
            f[i]=max(f[max(i-2,0ll)]+a[i],max(f[max(i-2,0ll)],a[i]));
            ans=max(ans,f[i]);
        }
        cout<<ans<<'\n';
    }
    return 0;
}

CF1844D

考虑 nn 分解质因数为 x∗yx*y 的意义，一定表示第 ii 和第 i+x,i+yi+x,i+y 不能相同颜色，直接从2开始试除，除不动的时候就可以是原来的数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include<bits/stdc++.h>

#define lowbit(x) (x&(-x))

using namespace std;

const int maxn=500200;
int n,m,q,a[maxn];
int rk[maxn],cnt,kr[maxn];
int c[maxn];
int tot1,mmx;

void add_tree(int x,int y)
{
    while(x<=n)
    {
        c[x]+=y;
        x+=lowbit(x);
    }
}

int query_tree(int x)
{
    int ans=0;
    while(x)
    {
        ans+=c[x];
        x-=lowbit(x);
    }
    return ans;
}

int main()
{
    ios::sync_with_stdio(false);
    cin>>n>>m>>q;
    set <int> looker;
    for(int i=1;i<=n;i++)
    {
        char t;
        cin>>t;
        a[i]=t-'0';
    }
    int t1,t2;
    for(int i=1;i<=n;i++) looker.insert(i);
    for(int i=1;i<=m;i++)
    {
        cin>>t1>>t2;
        for(auto it =looker.lower_bound(t1);it!=looker.end()&&*it<=t2;it=looker.erase(it))
        {
            rk[*it]=++cnt;
            kr[cnt]=*it;
        }
    }
    mmx=cnt;
    for(int i=1;i<=n;i++)
    {
        if(!rk[i]) rk[i]=++cnt,kr[cnt]=i;
    }
    for(int i=1;i<=n;i++)
    {
        if(a[kr[i]]) 
        {
            tot1++;
            add_tree(i,1);
        }
    }
    for(int i=1;i<=q;i++)
    {
        int tmp;
        cin>>tmp;
        if(a[tmp]) tot1--;
        else tot1++;
        a[tmp]^=1;
        add_tree(rk[tmp],a[tmp]?1:-1);
        cout<<min(mmx,tot1)-query_tree(min(mmx,tot1))<<'\n';
    }
    return 0;
}

20230712

CF1847D

给你一个 01 串，我们用他的某些子串拼成串 T ，你可以交换原来的串的 0 和 1，为了让 T 字典序最大，你至少要交换多少次？

我们很显然有个贪心是先满足前面的串全 1 ,这个时候我们可以定义某个位置的优先度，由于是从做到右，我们可以从左到右赋予它优先度。这里可以用一个 set 来做。

然后就假设我们当前有 x 个 1，那么我们一定是把这 x 个 1 给优先度为前 x 的个数的东西。用一个树状数组来做就好了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include<bits/stdc++.h>

#define lowbit(x) (x&(-x))

using namespace std;

const int maxn=500200;
int n,m,q,a[maxn];
int rk[maxn],cnt,kr[maxn];
int c[maxn];
int tot1,mmx;

void add_tree(int x,int y)
{
    while(x<=n)
    {
        c[x]+=y;
        x+=lowbit(x);
    }
}

int query_tree(int x)
{
    int ans=0;
    while(x)
    {
        ans+=c[x];
        x-=lowbit(x);
    }
    return ans;
}

int main()
{
    ios::sync_with_stdio(false);
    cin>>n>>m>>q;
    set <int> looker;
    for(int i=1;i<=n;i++)
    {
        char t;
        cin>>t;
        a[i]=t-'0';
    }
    int t1,t2;
    for(int i=1;i<=n;i++) looker.insert(i);
    for(int i=1;i<=m;i++)
    {
        cin>>t1>>t2;
        for(auto it =looker.lower_bound(t1);it!=looker.end()&&*it<=t2;it=looker.erase(it))
        {
            rk[*it]=++cnt;
            kr[cnt]=*it;
        }
    }
    mmx=cnt;
    for(int i=1;i<=n;i++)
    {
        if(!rk[i]) rk[i]=++cnt,kr[cnt]=i;
    }
    for(int i=1;i<=n;i++)
    {
        if(a[kr[i]]) 
        {
            tot1++;
            add_tree(i,1);
        }
    }
    for(int i=1;i<=q;i++)
    {
        int tmp;
        cin>>tmp;
        if(a[tmp]) tot1--;
        else tot1++;
        a[tmp]^=1;
        add_tree(rk[tmp],a[tmp]?1:-1);
        cout<<min(mmx,tot1)-query_tree(min(mmx,tot1))<<'\n';
    }
    return 0;
}

20230713

CF1844E. Great Grids

每个 2*2 方格有三种字母，并且保证相邻的不相同，现在限制某些格子对之间必须相同，询问是否存在这个合法的 n*m 的方格。

其实画图就可以发现，如果是要求对角相同，这个 2*2 的格子一定只有这4种情况（ a,b,c 分别代表模 3 意义下的 0,1,2）.

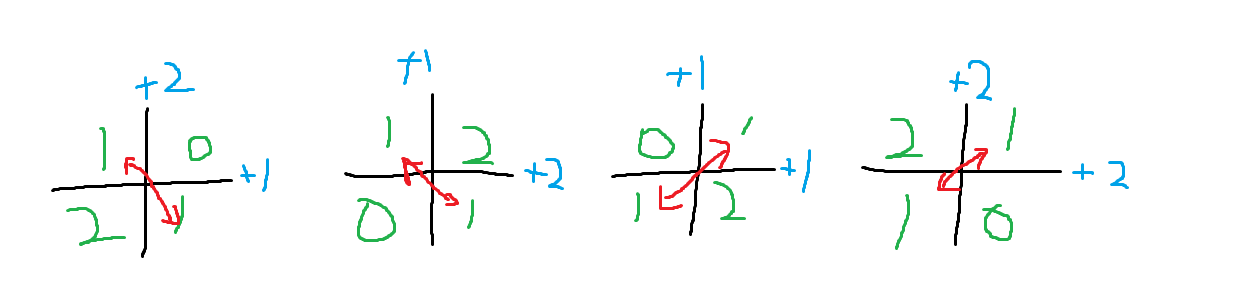
pC4bc79.png

此刻考虑把这个中心竖轴和横轴抽象为四个点，r1,r2,c1,c2 。分别代表列 +1,+2 行 +1,+2 ，对于有这种要求对角线要求的格子，如图所示，对于左上=右下，连 r2->c1,r1->c2 对于右上=左下，连 r1->c1,r2->c2 。 一旦 r1,r2 或者 c1,c2 在一个并查集了，说明不可能存在这个方格。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include<bits/stdc++.h>

using namespace std;

const int maxn=10010;

int n,m,q,f[maxn],T;

int getf(int x)
{
    if(f[x]==x) return x;
    return f[x]=getf(f[x]);
}

void merge(int x,int y)
{
    x=getf(f[x]);
    y=getf(f[y]);
    f[x]=y;
}

int main()
{
    ios::sync_with_stdio(false);
    cin>>T;
    while(T--)
    {
        
        cin>>n>>m>>q;
        for(int i=1;i<=n*2+m*2;i++) f[i]=i;
        for(int i=1;i<=q;i++)
        {
            int t1,t2,t3,t4;
            cin>>t1>>t2>>t3>>t4;
            if(t1>t3)
            {
                swap(t1,t3);
                swap(t2,t4);
            }
            if(t2<t4)
            {
                merge(t1,t2+n*2+m);
                merge(t1+n,t2+n*2);
            }
            else
            {
                merge(t1,t4+n*2);
                merge(t1+n,t4+n*2+m);
            }
        }
        int bj=0;
        for(int i=1;i<=n;i++)
        {
            if(getf(i)==getf(i+n)) 
            {
                cout<<"NO\n";
                bj=1;
                break;
            }
        }
        if(bj) continue;
        for(int i=1;i<=m;i++)
        {
            if(getf(i+n*2)==getf(i+n*2+m)) 
            {
                cout<<"NO\n";
                bj=1;
                break;
            }
        }
        if(bj) continue;
        cout<<"YES\n";
    }
}

20230714

CF1844F1

给你一个数组 aa ，对其任意排序得到数组 bb ，试着最小化 S=∑i=1n−1∣bi+1−bi−c∣S= \sum_{i=1}^{n-1}\limits|b_{i+1}-b_i-c| ，同时满足 bb 字典序最小。

显然对于 c≥0c \geq 0 的情况，从小到大排序即可。

对于 c<0c<0 情况，可以保证从大到小一定是最优的。

例如，我们现在有 x>y>zx>y>z ,我们取两个排布，例如 xyz,xzy，写出它们的s1=∣y−x−c∣+∣z−y−c∣,s2=∣z−x−c∣+∣y−z−c∣s1=|y-x-c|+|z-y-c|,s2=|z-x-c|+|y-z-c| ，由于z−x=z−y+y−zz-x=z-y+y-z ,代入原式则有 s2=∣y−x−c+(z−y)∣+∣y−z−c∣s2=|y-x-c+(z-y)|+|y-z-c| 由于 z<yz<y ，一定有 (z−y)−c<−c(z-y)-c<-c ， 也就是 s1<s2s1<s2 ，同理可以推出其他情况。

证明他是最优的，我们接下来就是找字典序最小的，这个简单贪心就能做了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include<bits/stdc++.h>

#define int long long

using namespace std;

const int maxn=5050;
const int looker=-1e18;

int n,T,f[maxn],ans,a[maxn],b[maxn];
int c;


signed main()
{
    ios::sync_with_stdio(false);
    cin>>T;
    while(T--)
    {
        cin>>n>>c;
        for(int i=1;i<=n;i++) cin>>a[i];
        if(c<0) sort(a+1,a+n+1,greater<int>());
        else sort(a+1,a+n+1);
    	//find a place to change
        if(c>=0)
        {
            for(int i=1;i<=n;i++) cout<<a[i]<<" ";
            cout<<endl;
            continue;
        }
        for(int i=1;i<=n;i++)
        for(int j=n;j>i;j--)
        {
            int bascost=0,nowcost=0;
            if(j<n) bascost+=abs(a[j+1]-a[j]-c);
            bascost+=abs(a[j]-a[j-1]-c);
            if(i>1) bascost+=abs(a[i]-a[i-1]-c);
            nowcost+=abs(a[i]-a[j]-c);
            if(i>1)nowcost+=abs(a[j]-a[i-1]-c);
            if(j<n) nowcost+=abs(a[j+1]-a[j-1]-c);
            if(bascost==nowcost)
            for(;j>=i+1;j--) swap(a[j],a[j-1]);
        }
		for(int i=1;i<=n;i++) cout<<a[i]<<' ';
		cout<<endl;
    }
    return 0;
}

20230715

1845D - Rating System

题目大意：给你一段差分序列，当序列前缀和大于等于 kk 时候，后面数不会低于 kk ，试求出 kk 使得序列最后一位最大。

显然要达到了才能 kk 才有意义，把序列分成两段，前一段前缀和大于kk,右边另外考虑，比如右边是序列 −100,2,4,−5,3,1-100,2,4,-5,3,1 ,我们设 g(x)>0g(x)>0 表示 [x,n][x,n] 能够增加的个数。

我们从后向前推，g(x)=[5,5,4,4,4,1]g(x)=[5,5,4,4,4,1] 显然，这个可以用一个栈结构来维护，栈底（特判小于 0 情况）即g(x)g(x)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include<bits/stdc++.h>

#define int long long
#define lowbit(x) (x&(-x))

using namespace std;

const int maxn=300200;

int n,a[maxn],s[maxn],c[maxn],T,ans,ansk;
int st[maxn],top,g[maxn];

// struct tree_array{

//     void add_array(int x,int y)
//     {
//         while(x<=n)
//         {
//             c[x]+=y;
//             x+=lowbit(x);
//         }
//     }

//     int query_array(int x)
//     {
//         int ans=0;
//         while(x)
//         {
//             ans+=c[x];
//             x-=lowbit(x);
//         }
//         return ans;
//     }

// }t;

signed main()
{
    ios::sync_with_stdio(false);
    cin>>T;
    while(T--)
    {
        cin>>n;
        for(int i=1;i<=n;i++)
        {
            cin>>a[i];
            s[i]=s[i-1]+a[i];
            c[i]=0;
        }
        // for(int i=1;i<=n;i++)
        // {
        //     if(a[i]>0) t.add_array(i,a[i]);
        // }
        ans=0,ansk=0;
        top=0;
        for(int i=n;i;i--)
        {
            st[++top]=a[i];
            while(top>1&&st[top]+st[top-1]>0&&st[top]>0)
            {
                st[top-1]+=st[top];
                top--;
            }
            g[i]=max(st[1],0ll);
            if(ans<s[i-1]+g[i])
            {
                ans=s[i-1]+g[i];
                ansk=s[i-1];
            }
        }
        // for(int i=1;i<=n;i++)
        // {
        //     if(s[i]+t.query_array(n)-t.query_array(i)>ans)
        //     {
        //         ans=s[i]+t.query_array(n)-t.query_array(i);
        //         ansk=s[i];
        //     }
        // }
        cout<<ansk<<'\n';
    }
}

CF1842D. Tenzing and His Animal Friends