前言

按照 CSAPP 学习。由于本人具备了一定的基础，所以写的不会很详细。

Integers

二进制，没有什么好说的。long double 在 x86-64是 10 或者 16 位。

乘法需要三个周期，而加法只需要一个，除法需要30+。

$2^{10} \approx 10^3$ 以此类推，可以快速确定一个数字的位数。

uint 与 int 比较的时候，是 int 转 uint 所以 uint<=-1

Big Endian 与 Little Endian

例如表示 0x01234567 前者是01 23 45 67 后者是67 45 23 01 有的机器是前者方式，有些机器是后者方式。但在2024年，你很难买到前者了，换句话说都是倒过来的，即Little Endian

Floating Point

对于一个数字，二进制下表示先转化为 $1.xxxxxxxxx*2^{exp}$

下文中,阶码表示为exp,尾数表示为 frac

类型	长度	符号位	exponent(阶码)	fraction（尾数）
float	32bits	1	8	23
double	64bit	1	11	52
Extend precision（Intel 私有）	80bits	1	15	63/64

对于一般情况

当 Exp 不是全 0或者全 1 的时候：
$x=(-1)^{S}*M*2^{E}$ 其中 $E=Exp-Bias$

$Bias =2^{k-1}-1$ , $k$ 代表阶码，例如在 float 数据结构中, $k=8,Bias=2^7-1=127$

对于 $M$ ，即为转化为 $1.xxxxx*2^{E}$ 的数字后剩下的 xxxxx,因此其最小值在全0 取，此时左边变成 $1.0$ ，最大在全 $1$ 时候取，左边变成 $2.0-\epsilon$ (取决于数据类型)

例如，对于F=15213.0，在一个float中

/	内容
真实值	`1.1101101101101 *(2^13)`
M	`1.11011011011010000000000`(补足23位)
Exp	`1001100` (即为13+127)
完全表示	`0`+`1001100`+`11011011011010000000000`

现在，在一个float中, $0\leq Exp \leq 255$ ，此时，实际的 $-127 \leq E \leq 128$

(这里M在计算机中存储的是小数点后23位)

对于非标准化情况

实际上,你还会见到 Nan,inf,-0.0与0.0这种情况

exp=00…0

E = 1-Bias ，此时数字的绝对值小于 1

如果 frac 部分也是全0的情况 ,此时代表0,由于没有补码这种操作，因此会出现 $\pm 0$ 两种情况

对于 frac 部分不为 0 的话,表示接近 0 的小数,并不是所有的0.xxx 的小数都是这样表示,例如定义一个 8bit,1s,4exp,3frac 的 Mloat,非标准化下 E=1-7=-6,此时非标准下的 0 0000 111 表示 7/512,但是标准表示下的 0 0001 000 ,bias=2^{k-1}-1 = 6,E=exp-bias=1-7=-6 ,原来的数字就是1.0*2^{-6}=8/512

exp = 1111

如果 frac 全 0 ,此时表示正负无穷大(看符号位)

如果 frac 不是全 0 ,此时表示 Not-a-Number(Nan),一般情况下 sqrt(-1) , $\infty-\infty$ 等操作会出现

小结

这种表示方式在 0 附近能表示最多的数,一旦数字很大时误差就很大,作为参考 6bit,1s,2exp,3frac 大概会长这样。

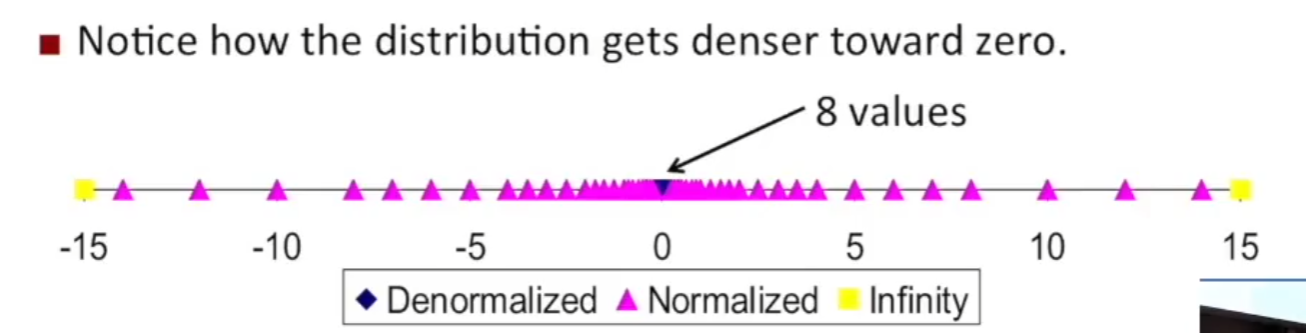
因为我们exp 每次加 1 的时候（除了全0），误差都会增加一倍。

浮点数的运算。

简单来说，就是x+ (float)y = Round(x+y),x *(float)y=Round(x*y)

进位

由于浮点数表达方法和整数区别很大，比如浮点数没有补码这个概念，并且有exp 等概念，使其和普通的整数运算区别很大，并且由于精度有限，还需要保留位数。比如Round up,Round down,Towards zero,Nearest Even等。Nearest Even 是默认方法，向偶数舍入。这里并不是说1.40 = 1.50 = 2 ，而是仅当小数位为 0.5 的时候，向最近的偶数，其他情况和四舍五入相同。

7.8949999->7.89
7.8950000->7.90
7.8950001->7.90
7.8850000->7.88
//以下为二进制
10.11100->11.00
10.10100->10.10

在二进制视角下，最近偶数实际上是这样的：

1 2	1.1->0.0(进位) 0.1->0.0

乘法

对 $x_1=(-1)^{s_1}*M_{1}*2^{E_1},x_2=(-1)^{s_2}*M_{2}*2^{E_2}$

操作流程为

S_new = s1^s2
M_new = M_1*M_2
E_new = E^1+E^2
if M_new>=2 :
    右移，增加E
if E_new 超过了最大能表示的 :
    overflow
对M_new 保留 frac 位的位数

对比整数

加法交换律

1 2	(3.14+1e10)-1e10=0 3.14+(1e10-1e10)=3.14

浮点加法数不满足结合律，其他情况下浮点数字几乎拥有整数加法的所有特性（例外是NaN,inf）

乘法分配律

由于不满足交换律，分配律自然也不满足。

转化：

double->int， frac 最多保留 31 位，并且有可能放不下。（还得看exp）

float->int，虽然frac 小于 31 ，但是还要看frac

int->float 可能会出现保留位数

int->duble 能放下，因为frac有52位。

Machine Level Programming

basis

Compare

Procedures

Data

Array Allocation

整数数组在内存中的存储

没什么可以写的，仅需注意，当定义数组 val[5] 时，假设 val 地址为 x ，有 val+1=x+4 。

Advanced topics

汇编语言

寄存器

C语言中的类型与汇编中联系

（AT&T）

C	汇编类型	汇编后缀	长度(byte)
char	Byte	b	1
short	Word	w	2
int	Double word	l	4
long	Quad word	q	8
char *	Quad word	q	8
float	Single precision	s	4
double	Double precision	q	8

|C|汇编类型|汇编后缀|长度(byte)|
|-|-|-|-|
|char|Byte|b|1|
|short|Word|w|2|
|int|Double word|l|4|
|long|Quad word|q|8|
|char *|Quad word|q|8|
|float|Single precision|s|4|
|double|Double precision|q|8|

例如区别 movb,movw,movl,movq 分别代表mov 1,2,4,8 bytes 操作

上面的汇编格式Intel的语法。常见的汇编有两种语法，一种是Intel，另一种是AT & T。 Intel的格式是 opcode destination, source，类似于语法 int i = 4；而AT & T的格式是opcode source, destination，直观理解为 move from source to destination。
(引用自如何阅读简单的汇编)

指令

指令	功能
`MOV A,B`	将 B 赋值给 A
`LOAD A,B`	将存储单元 B 复制寄存器 A
`STORE A,B`	将寄存器B 复制到存储单元A
`ADD A,B`	AB相加，最后值赋给A
`TEST A`	测试A是否为0
`BEQ Z`	如果最后一次TEST为True，执行Z处代码

|指令|功能|
|-|-|
|`MOV A,B`|将 B 赋值给 A |
|`LOAD A,B`|将存储单元 B 复制寄存器 A |
|`STORE A,B`|将寄存器B 复制到存储单元A|
|`ADD A,B`|AB相加，最后值赋给A|
|`TEST A`|测试A是否为0|
|`BEQ Z`|如果最后一次TEST为True，执行Z处代码|