Digital VLSI Design-lecture 4
Lecture 4: Logic Synthesis Part 2
在 lec3 的学习中,我们已经知晓了编译和库。我们已经将设计加载到综合器中,也加载了标准单元库和IP。
接下来我们要讨论综合过程中更核心的部分。
布尔最小化
布尔最小化是综合过程中的一个关键步骤,涉及将逻辑表达式简化为最小形式,以优化电路设计。
展开和绑定和预映射优化
在这个步骤中,工具将执行以下操作
- 将 RTL 编译为布尔数据结构
- 将非布尔模块绑定到叶单元
- 优化布尔逻辑
将设计结果映射到通用的、与技术无关的逻辑门。
这是逻辑综合的核心,自八十年代一直研究的主题。

Two-Level Logic
在展开过程中,主要输入和输出(端口)被定义,顺序元素(触发器、锁存器)被推断。这导致了一组组合逻辑云:
- 输入端口和寄存器输出是逻辑的输入。
- 输出端口和寄存器输入是逻辑的输出。
- 输出可以描述为输入的布尔函数。
- 布尔最小化的目标是减少输出函数中的文字数量。
许多不同的数据结构都能用来表示布尔函数,如真值表、立方体、二元决策图、方程等。
许多研究是基于SOP或POS表示法进行的,这种表示法更为人知的是“两级逻辑”(Two-Level Logic)
Two-Level Logic Minimization
卡诺图是一个变形的真值表,它能简化逻辑函数,但是:
- 问题自动化困难,例如 NPC
- 单元格数量呈指数增长
Quine-McCluskey方法虽然在软件中易于实现,但是计算复杂度过高。
Espresso启发式最小化器
SOP解指的是“与或形式”(Sum of Products)的表达方式。在数字逻辑中,SOP是一种标准化的布尔表达式形式,其中多个乘积项(与项)通过加法(或运算)组合在一起。每个乘积项由变量的与运算构成,可以是变量本身或其否定。
例如,布尔表达式 就是一个SOP形式,其中 和 是乘积项。
- 我们从一个SOP解开始,按照以下步骤:
- 扩展(Expand)
- 在不覆盖OFF集中的点的情况下,使每个立方体(矩形)尽可能大。
- 增加文字数量(更差的解)。
- 无冗余(Irredundant)
- 去除冗余立方体。
- 移除被更大立方体(矩形)覆盖的小立方体。
- 缩减(Reduce)
- 覆盖中的立方体(矩形)被缩小。
- 通常,新覆盖将与初始覆盖不同。“扩展”和“无冗余”步骤可能会找到覆盖ON集点的新方法。希望新覆盖会更小。
- 扩展(Expand)
我们来看一个优化的例子:
多级逻辑最小化
两级逻辑已经被广泛研究,且有许多著名的方法,两级逻辑通常指简单的与或非门组合。
但是多级逻辑可能更好或者更实用,这种方法允许使用多个逻辑层次来优化电路设计。
以下是一个多级逻辑最小化的例子。减少了逻辑门数量和深度,文字数量等。
Binary Decision Diagrams (BDD)
BDD 是一种用于表示布尔函数的有向无环图。它们通过节点和边来表示真值表中的逻辑关系。
Shannon扩展定理是构建二叉决策图(BDD)的基础。它通过将布尔函数分解为更简单的子函数(余因子)来实现。
Shannon扩展定理
给定一个布尔函数 通过以下方式分解。
- 正余因子 :当变量 时候函数值
- 负余因子 :当变量 时候函数值
对于
,
显然, 包含了 情况
这样,我们就得到了个BDD的表示形式
Reduced Ordered BDD (ROBDD)
由于BDD会变得非常大,我们要优化其中的表示
合并同类叶节点
这是最容易想到的规则,如图所示
合并同构节点
除了叶子节点,其他节点也可能同构,这些节点也能合并
消除冗余测试
如果实线( )虚线( ) 都指向一个位置,那这个节点根本没有必要存在。
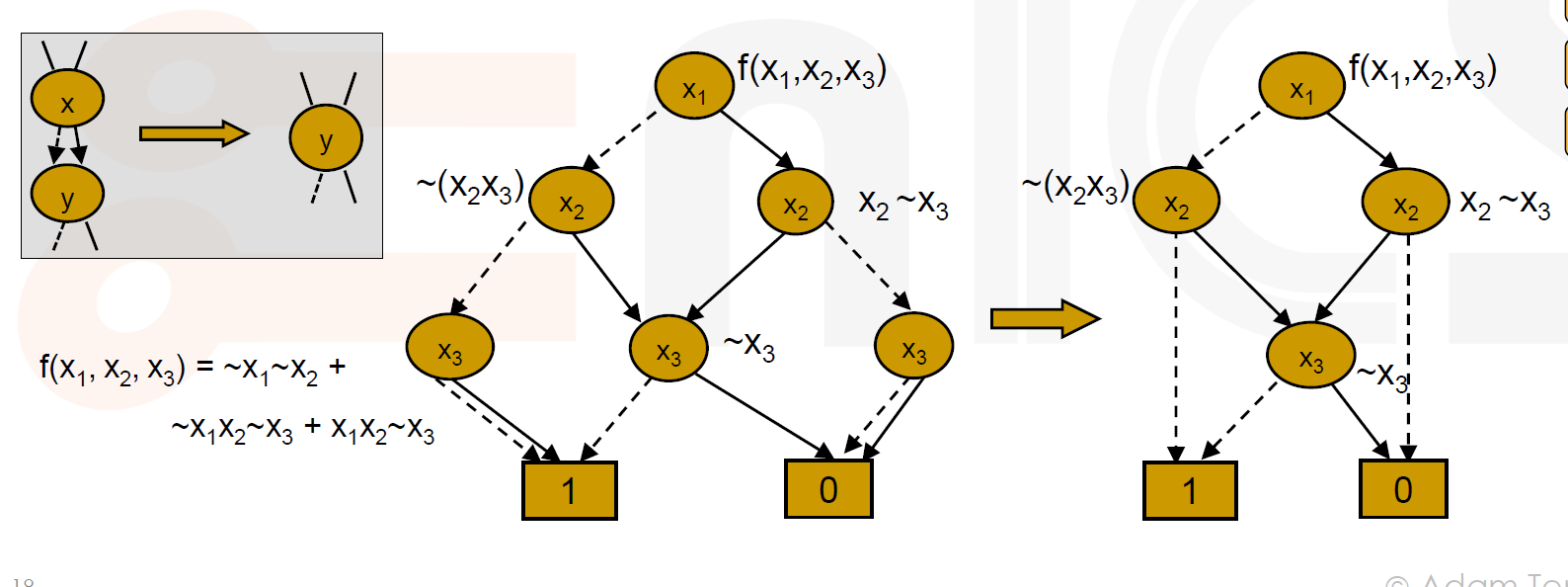
- 现在你已经优化好这个 BDD 了,接下来我们要介绍它的优点:
- BDD是常数 1 ,因此检查重言式是 trival
- 给定一个函数 的 BDD ,可以通过交换终端节点得到 的BDD
- 如果两个函数 在相同变量顺序下相同,则他们是等价的
- 你还需要注意以下情况
- 如果变量展开的顺序改变,BDD的大小可能会显著变化。
- 在最坏情况下,即使经过简化,BDD中的节点数量也可能是变量数量的指数级。
约束定义
在详细说明之后,设计被加载到综合工具中,并存储在数据结构中。可以通过名称访问分层端口(输入/输出)和寄存器。
1 | set in_ports [get_ports IN*] |
然后,可以加载 SDC 格式的约束
1 | read_sdc -verbose sdc/constraints.sdc |
例如,创建一个时钟并定义目标频率
1 | create_clock -period $PERIOD -name $CLK_NAME [get_ports $CLK_PORT] |
技术映射
Technology mapping 是逻辑综合的一个阶段,在这个阶段中,从技术库中选择门电路来实现电路。
- 为什么要进行技术映射?
- 直接实现可能效果不好,例如
F=abcdef实现为一个6输入的与门会导致较长的延迟 - 库中的门电路是预先设计的,通常在面积、延迟、功耗等方面进行了优化。
- 在关键路径上使用最快的门电路,在非关键路径上使用面积高效的门电路(组合)。
- 可以应用最小成本树覆盖算法来解决这个问题。
- 直接实现可能效果不好,例如
Technology Mapping Algorithm
使用递归树覆盖算法(recursive tree covering algorithm),可以轻松且几乎最优地将逻辑网络映射到技术库。
- 该过程包含三个步骤:
- Map netlist and tech library to simple gates
- 用仅包含 NAND2 和 NOT 门的方式描述网表。
- 用 NAND2 和 NOT 门描述 SC 库,并为每个门关联一个成本。
- Tree-ifying the input netlist、
- 树覆盖只能应用于树结构
- 在所有扇出大于 2 的地方分割树
- Minimum Cost Tree Matching
- 对于树中的每个节点,递归地找到该节点的最小成本目标模式
- Map netlist and tech library to simple gates
接下来,结合具体例子,来理解这个算法。
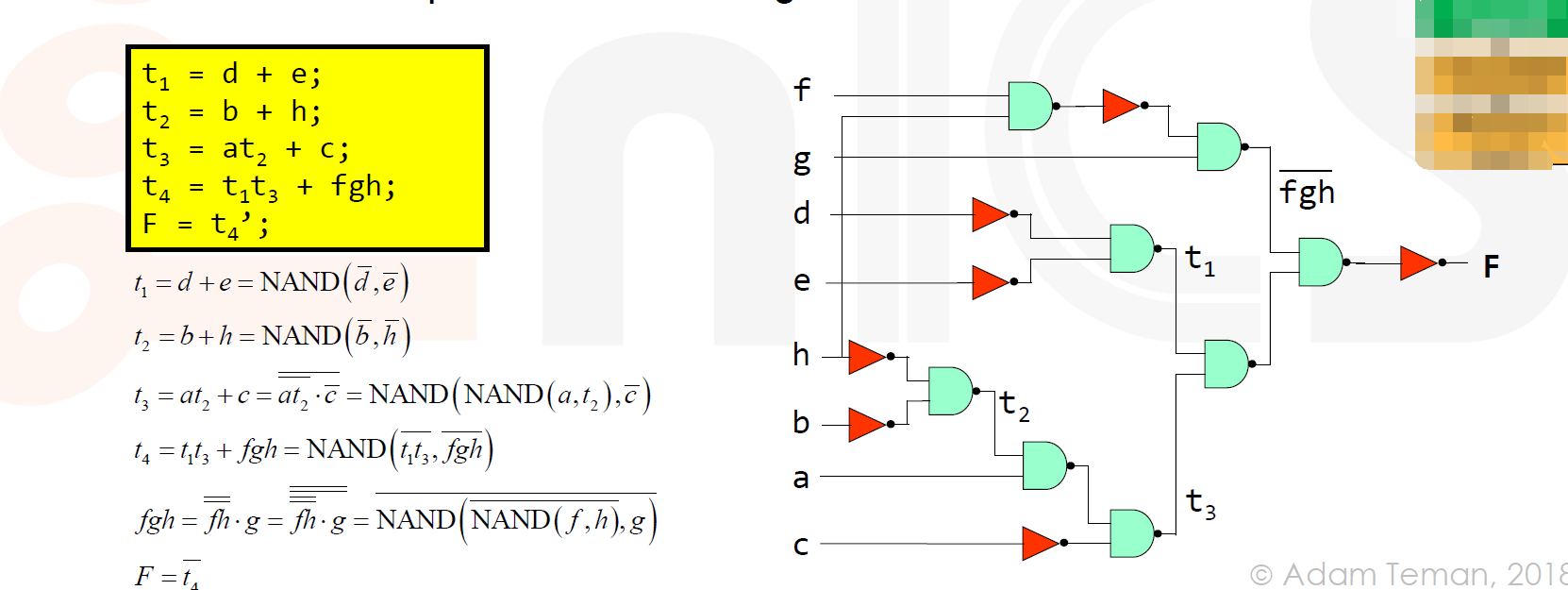
第一步是应用德摩根定律将布尔函数转换为 NAND2 和 NOT 门。
在一堆门,结合花销(功耗/延迟/面积),确定映射方法。同时,下面是一些通过 NAND2 和 NOT 门实现其他逻辑门的例子。
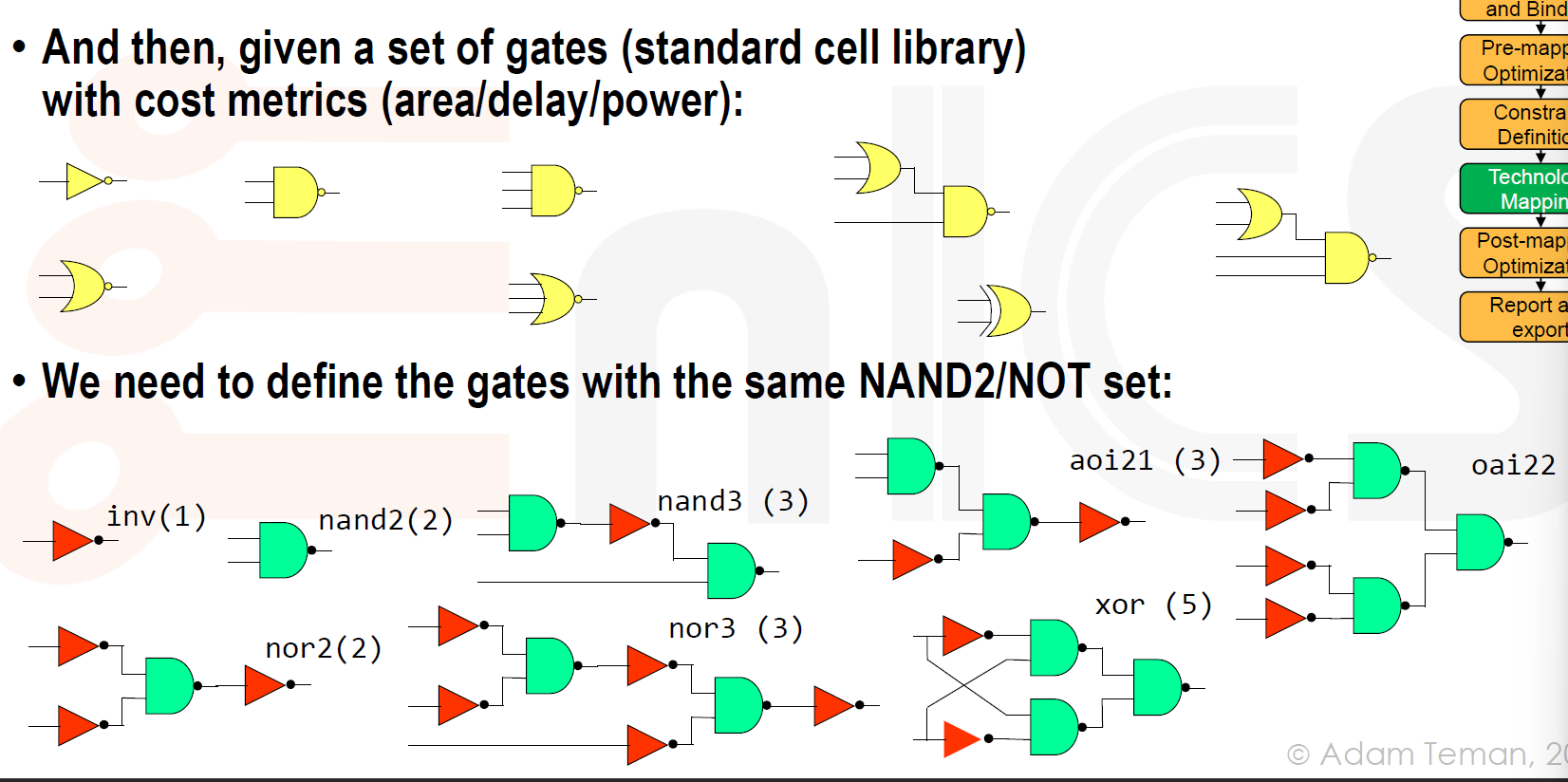
既然是应用树覆盖算法,我们需要在树上操作,但是我们给出的逻辑网络是树吗?
显然不是,因此需要在任何扇出大于 的地方打断树,以下是一个例子:
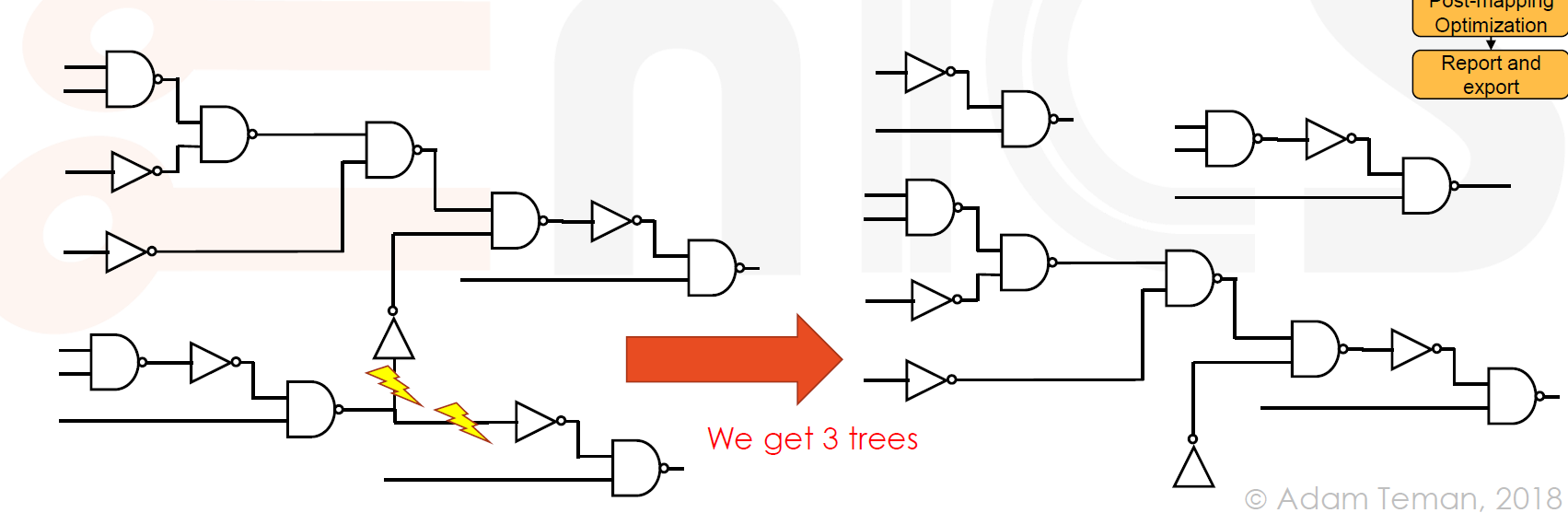
现在,我们才能够运行最小树覆盖,从图的输出开始,对于每个节点,找到所有匹配的目标模式
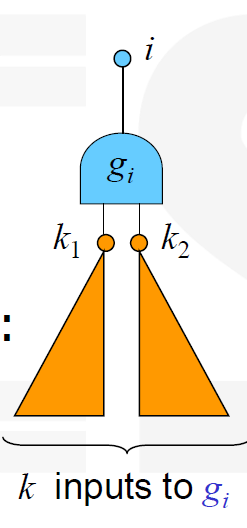
在一棵树上,使用门 ,我们有 $\text{cost}(i) = \min_k \left{ \text{cost}(g_i) + \sum_k \text{cost}(k_i) \right} $
表示的是门 的输入
Verilog 在综合中的作用
我们重新审视一下 Verilog 在综合的作用,以以下代码为例:
1 | always @(x) |
很容易设计出一个最朴素的电路:
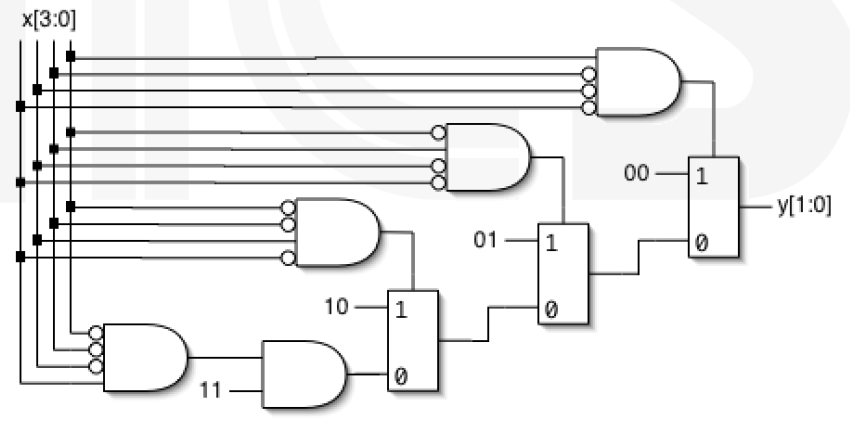
首先,代码可以用 case 而不是 if-else
1 | always @(x) |
设计的电路如下:
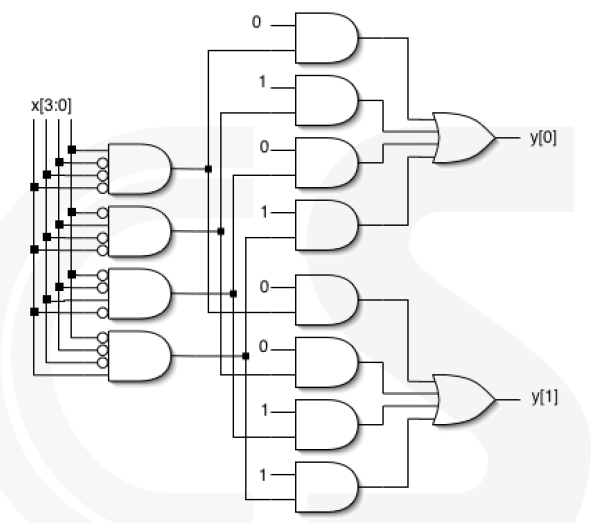
并且可以接着优化到以下情况:
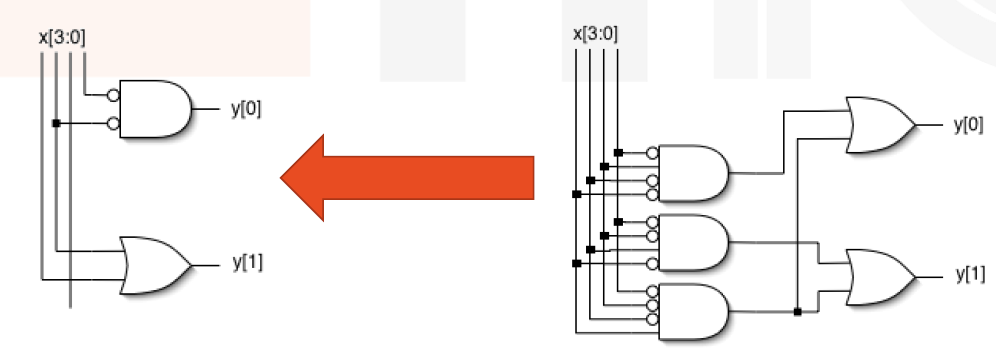
在上面的例子中,如果编码错误,我们会在逻辑仿真中传递一个 x ,如果保证是 one-hot 编码呢?
1 | always @(x) |
实际上,我们实现了一个“优先级编码器”(最低有效的‘1’优先)。
关于运算的说明
- 逻辑运算符映射为基本逻辑门
- 算术运算符映射为加法器、减法器等
- 无符号或有符号的二进制补码
- 模拟进位:目标比源宽一位
- 注意乘法、取模和除法
- 关系运算符生成比较器
- 常量位移只是线连接
- 不涉及逻辑
- 可变位移是完全不同的情况,需要移位器
- 条件表达式生成逻辑或多路复用器(MUX)
- 预编写的描述可以在 Synopsys DesignWare 或 Cadence ChipWare IP 库中找到。
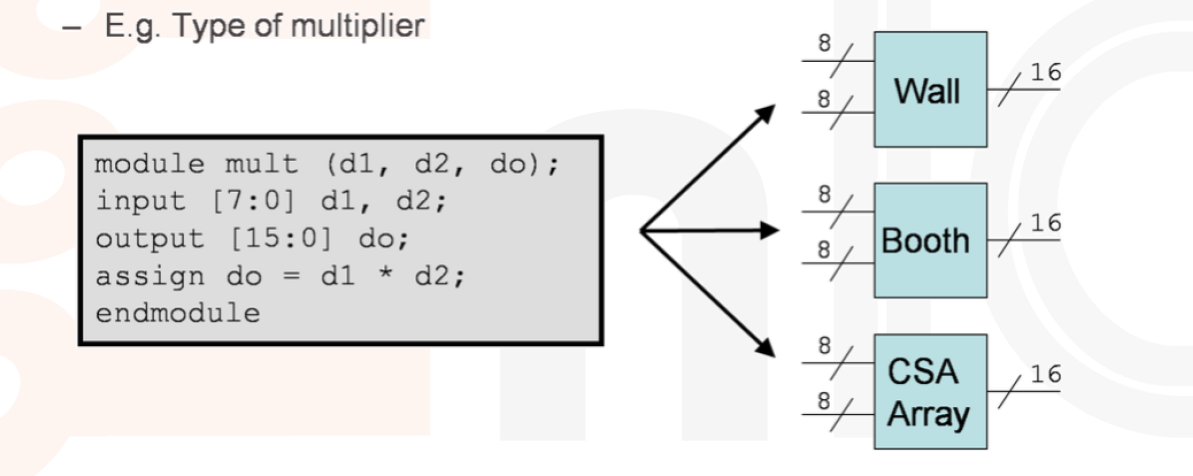
以上是一个乘法器的例子。
时钟门
由于时钟不断切换,它是动态功耗的主要消耗者,为了节省功耗,我们会尝试关闭未使用门的时钟。
- 时钟门分为块级(Global)和寄存器级(Local)
- 块级:如果某些操作模式不使用整个模块/组件,则应在 RTL 中定义时钟门控。
- 即使在寄存器级别,如果触发器的输出不变,内部功耗仍会因时钟切换而消耗。这在启用信号采样时非常典型,因此可以通过综合工具自动检测和门控。
三种方法可以实现门控:
- RTL 代码:显式指定时钟门控。
- 逻辑综合器:自动发现并实现局部门控机会。
- 时钟门控单元:在 RTL 中显式实例化。
但是对于 Global 级别来说,无法使用逻辑综合器,以下是时钟代码。
1 | // Conventional RTL Code |
Solution: Glitch-free Clock Gate
毛刺通常会出现在未使用锁存器的情况下。当使能信号(en)在时钟信号(clk)高电平期间发生变化时,可能会导致门控时钟(gclk)出现短暂的电压尖峰或不期望的脉冲。
为了解决时钟门控中的毛刺问题,可以在时钟的正相期间锁存使能信号。
1 | // 时钟门控,带有防毛刺锁存器 |
电路图如图所示
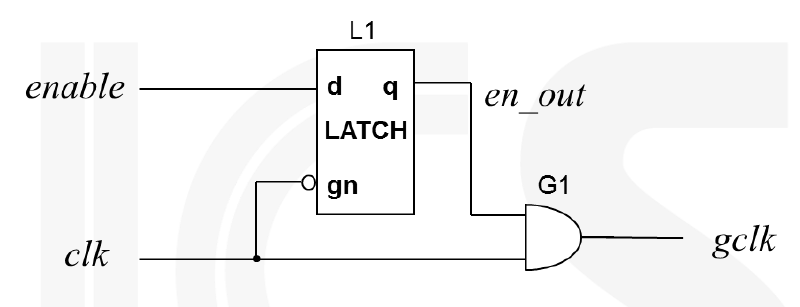
同时,我们可以合并具有相同使能信号的时钟门控,这可以降低时钟树工号,以及降低门控数量。
但是使能信号的时序和偏斜。
数据门控
在不需要的情况下,移位器(Shifter)和加法器(Adder)都在进行计算,即使结果未被使用。这会导致不必要的功耗。
通过数据门控,仅在需要时才进行计算。使用逻辑与操作符(&&)来控制输入信号,确保只有在需要时才激活移位器。
1 | assign add_out = A + B; |
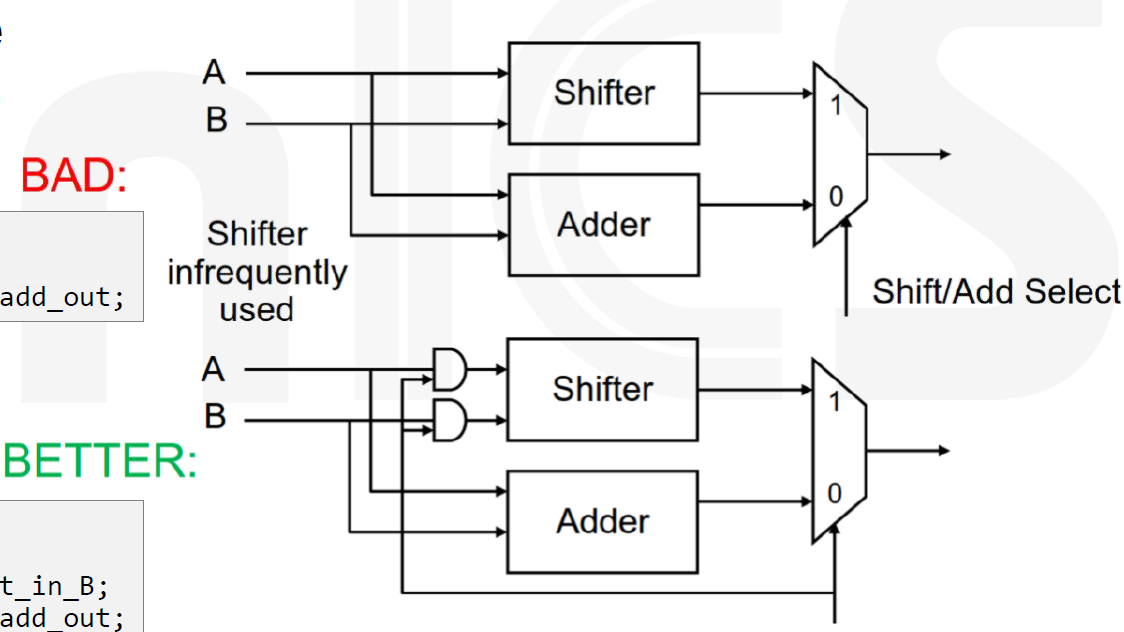
HDL 代码检查
HDL代码检查可提供快速简便的方式来检查可能代码不一致的问题:
- 仿真问题
- 综合问题
- 仿真与综合不匹配
- 时钟门控
- 锁存器推断
- 时钟域交叉问题
- 无意义的赋值/隐式位宽问题
不用于检查语法正确性,你可以你的仿真器来进行这项检查。或者,一些综合工具会给你基本的代码检查警告(针对仿真与综合不匹配错误)
时序优化
综合器会对逻辑进行转换,来改善成本函数
- 调整单元大小
- 缓冲或克隆以减少关键网络上的负载
- 分解大型单元
- 交换可交换引脚或等效网络之间的连接
- 将关键信号前移
- 填充早期路径
- 恢复面积
以下是一个双反相器移除变换的例子
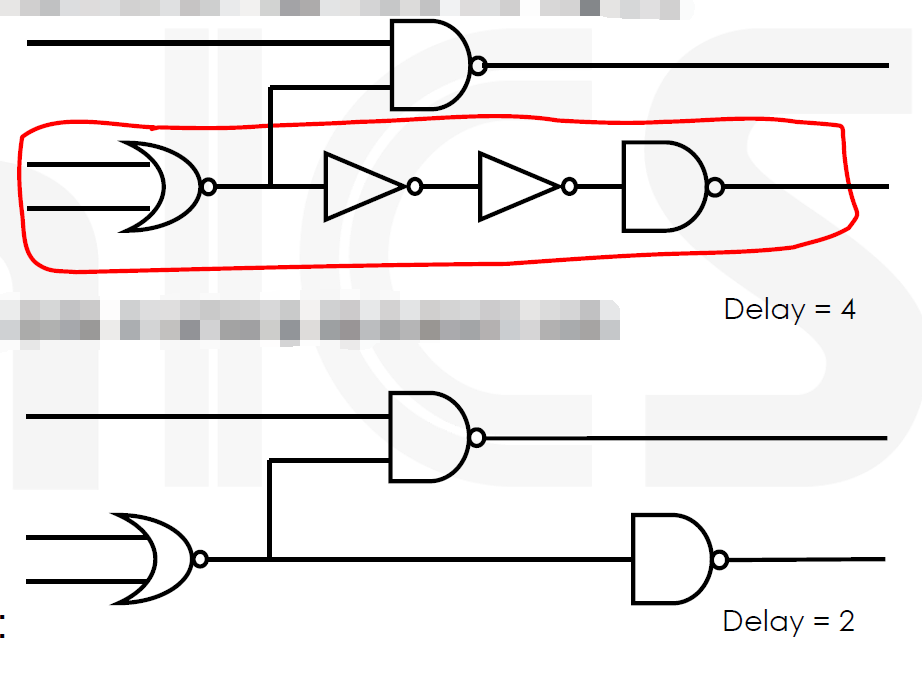
Resize
不同大小的门在不同负载下表现的延迟不同,例如有 A,B,C 三种门,在 0.7 负载下如下:
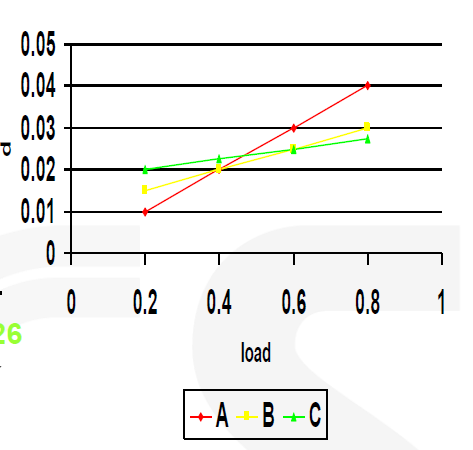
所以我们可以把 A 门换成 C 门

Copy
复制逻辑门以分担负载。通过创建门的副本(如 A 和 B),可以将负载分配到多个门上,降低每个门的负载压力。

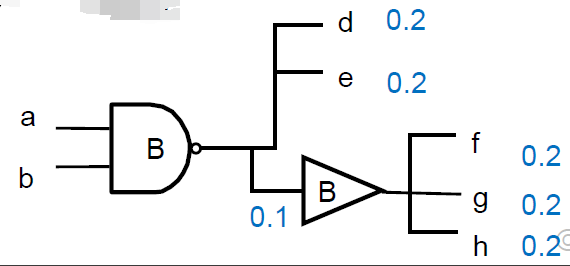
Buffer
在扇出网络中添加缓冲器,以改善信号传输。缓冲器(如 E)可以帮助减小延迟,提高信号完整性。
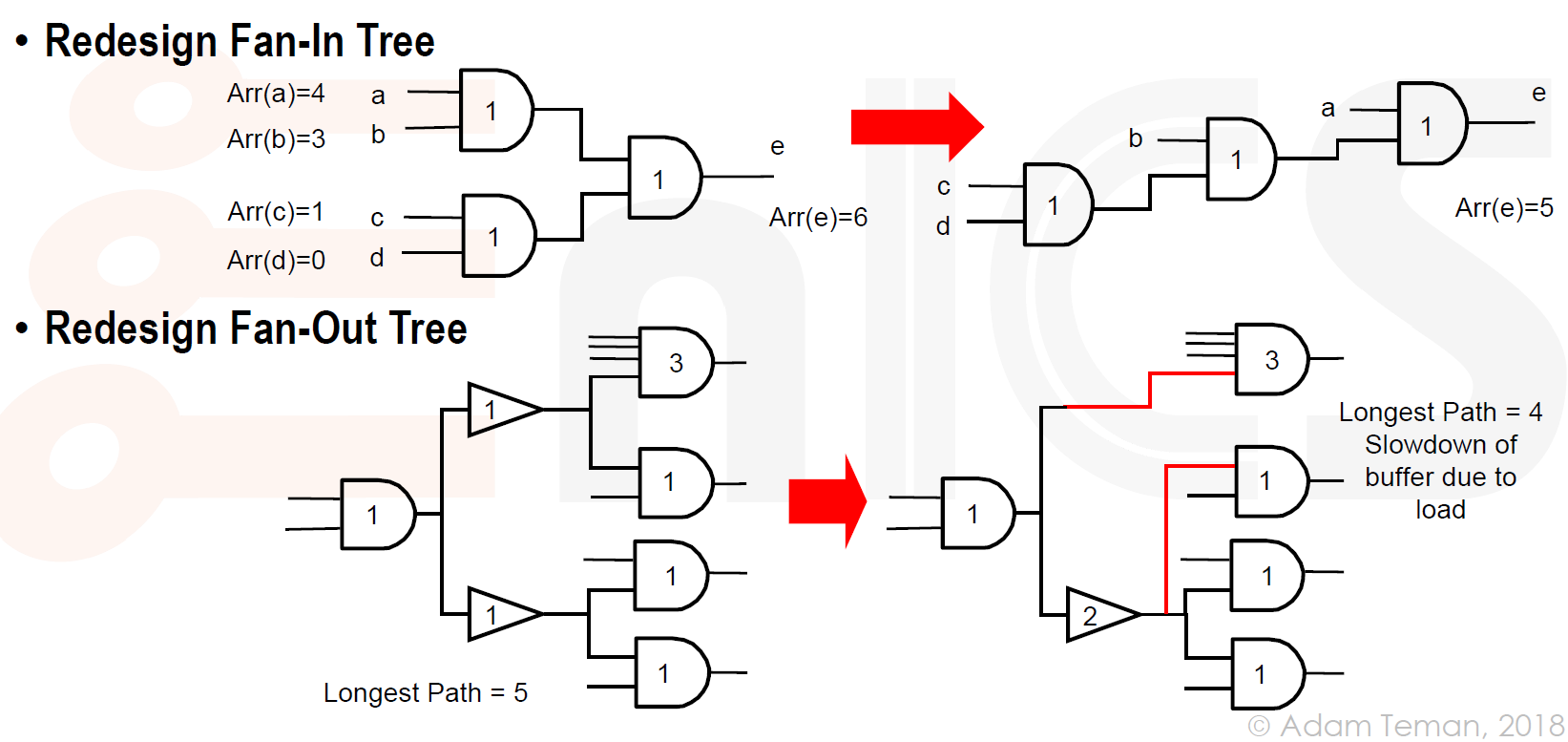
重新设计扇入/扇出树
信号从 a,b,c,d 传到 e ,耗时最后为 6 , 重构这棵树,可以实现更小耗时
同理,通过调整缓冲器和逻辑门的位置,扇出树减少了最长路径的长度到 4,
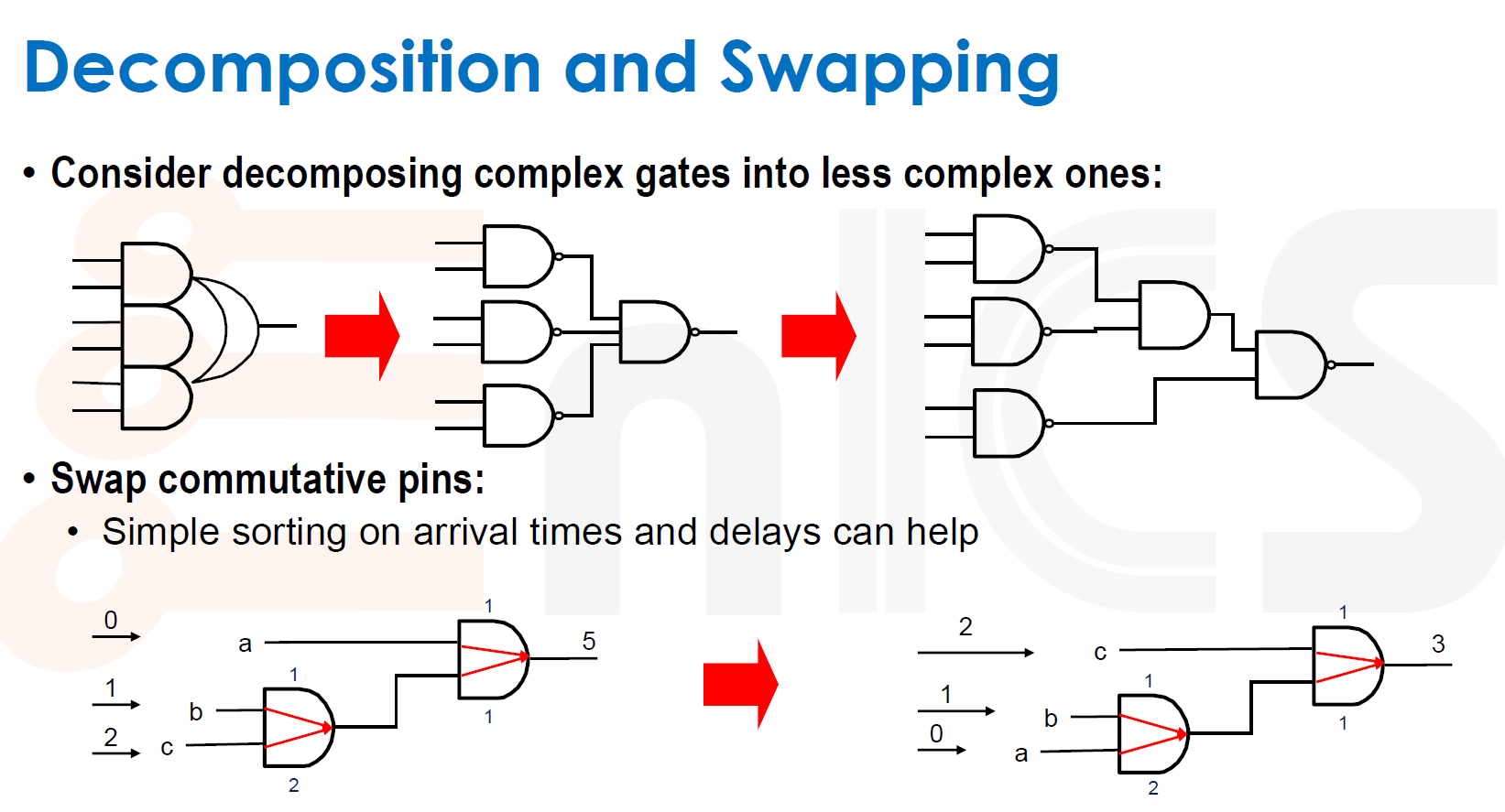
分解和交换
例如 a,b,c 的延迟是 0,1,2 在这幅电路中可以交换位置实现更小的延迟。
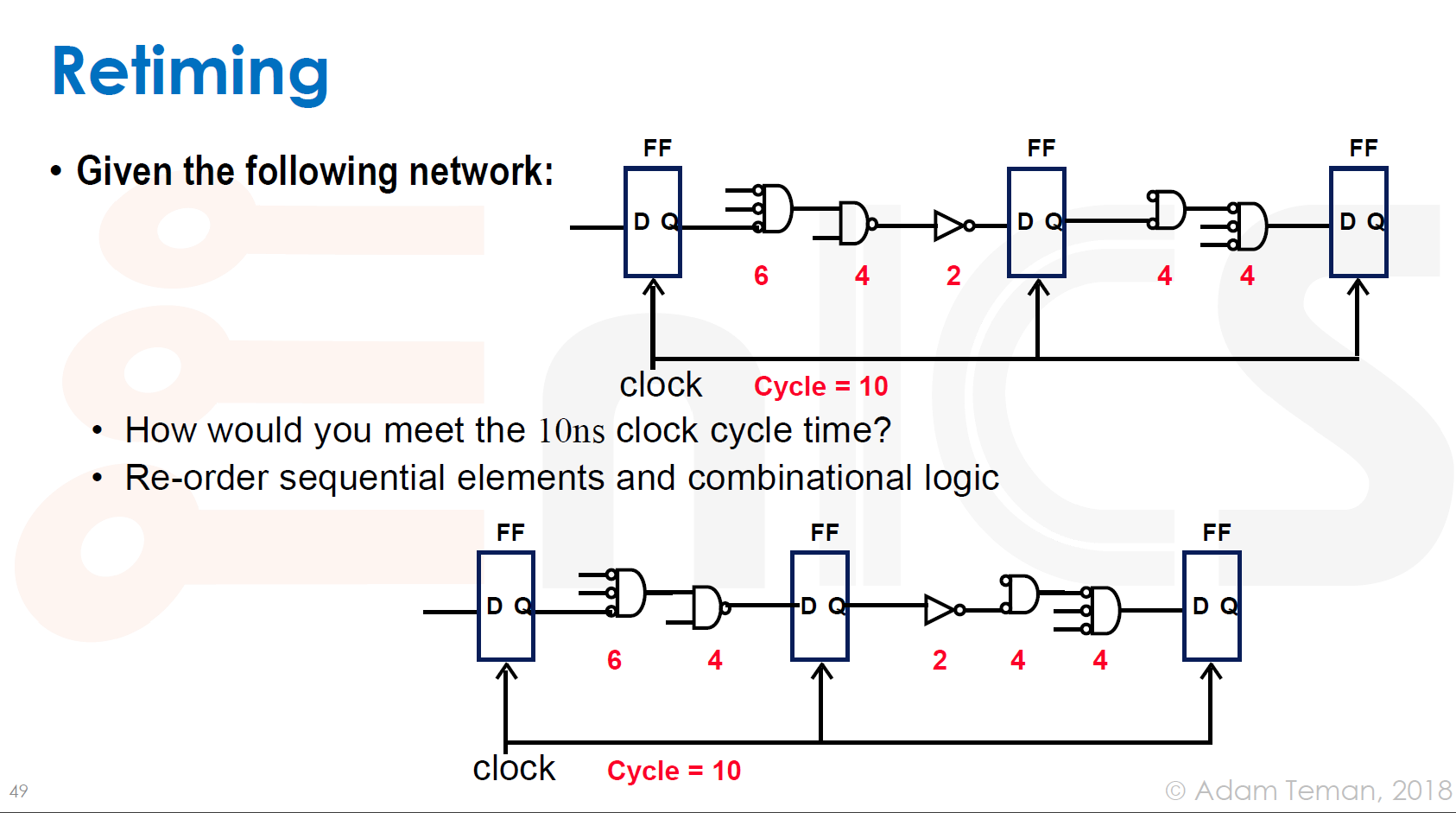
Retimming
从第一个触发器(FF)到最下一个触发器的路径延迟为 12ns和8ns ,如果我们要设计成10ns呢?
我们需要重新分配触发器位置
(完)










